机器学习：理论基础（四）—— 多元微积分

实际应用中的函数普遍包含多个变量，当进入高维时，微积分的普遍法则本质上保持原样，虽然必须引入一些新的记号，但幸运的是并不需要彻底改造原有理论，多变量微积分无非是同时在各个方向运用单变量微积分。

向量和矩阵表示法将大大简化多元微积分，并能保持与低维形式上的一致性，本文使用小写字母$x$表示标量，粗体小写字母$\boldsymbol{x}$表示向量，大写字母$X$表示矩阵。

1. 梯度（Gradient）

1.1 多元函数

定义：$f:\boldsymbol{x}\rightarrow y$，其中$\boldsymbol{x}=(x{1},x{2},…,x_{n})\in \mathbb{R}^{n}$，$y\in \mathbb{R}$，多元函数是从n维空间（n维向量）到一维空间（标量）的映射。

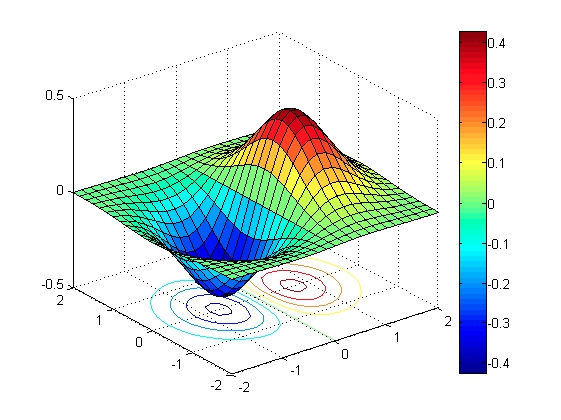
1.2 等高线图

定义：对于二元函数$f(x,y)$，曲线$f(x,y)=z{0}$称为函数f在平面$z=z{0}$中的等高线。如果所有等高线$z=z_{0}$都被投射到$x-y$平面上，则得到这个曲面的等高线图。

1.3 梯度（向量）

定义：$f$在点$\boldsymbol{x}$处的梯度是由对应维度的偏导构成向量，记作$\bigtriangledown f(\boldsymbol{x})$，读作grad f或del f。

$\triangledown f(\boldsymbol{x}) = \begin{bmatrix} \frac{\partial f}{\partial x_{i}} \end{bmatrix}_{n\times 1}$

性质：

梯度是标量对向量的导数；
梯度是输入空间中的一个偏导向量；
梯度的方向是在输入空间中使函数增长最快的方向；
梯度的大小是函数关于输入向量的最大变化率；
梯度也称为全导数，记做 $f^{‘}(\boldsymbol{x})$；

$f^{'}(\boldsymbol{x})=\triangledown f(\boldsymbol{x}) = \begin{bmatrix} \frac{\partial f}{\partial x_{i}} \end{bmatrix}_{n\times 1}\\ f(\boldsymbol{x}) \approx f(\boldsymbol{x_{0}})+f^{'}(\boldsymbol{x_{0}})^{T}(\boldsymbol{x}-\boldsymbol{x_{0}})$

1.4 全微分

定义：多元函数全增量$\triangle f$的线性主部，记做$df$。

$\begin{align*} \triangle f&=\sum_{i=1}^{n}a_{i}\triangle x_{i}+o(\rho )\\ df&=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}dx_{i} =\triangledown f(\boldsymbol{x})\cdot d\boldsymbol{x} \end{align*}$

梯度-全导数-全微分-偏导之间的关系如下：

$\triangledown f(\boldsymbol{x})=f^{'}(\boldsymbol{x})=\frac{\mathrm{d} f}{\mathrm{d} \boldsymbol{x}}=\begin{bmatrix} \frac{\partial f}{\partial x_{i}} \end{bmatrix}_{n\times 1}$

1.5 方向导数

定义：设$\mathbf{\mathit{u}}$为单位向量，$f$在该方向上的方向导数（变化率）记做$\frac{\partial f}{\partial \mathbf{\mathit{u}}}$。

$\begin{align*} \frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{u}}&=\lim_{h\rightarrow 0}\frac{f(\boldsymbol{x}+h\boldsymbol{u})-f(\boldsymbol{x})}{h}\\ &=\triangledown f(\boldsymbol{x})\cdot \boldsymbol{u}\\ &=|\triangledown f(\boldsymbol{x})|cos\theta \end{align*}$

性质：

方向导数是梯度向量在该方向上的投影；
梯度方向的方向导数最大，即函数在梯度方向上增长最快；
在负梯度方向上，函数下降最快；

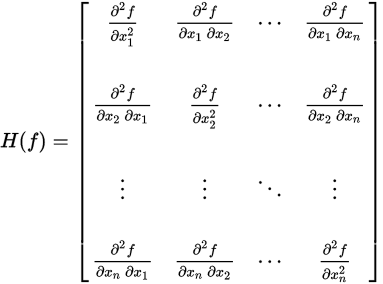
2. 海塞矩阵（Hessian Matrix）

定义：海塞矩阵是一个多元函数的二阶偏导数构成的对称方阵，描述了函数的局部曲率。

$H(f)=\begin{bmatrix} \frac{\partial f}{\partial x_{i} \partial x_{j}} \end{bmatrix}_{n\times n}$

完整写作：

2.1 多元泰勒展开

在工程实际问题的优化设计中，所列的目标函数往往很复杂，为了使问题简化，常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数。

$f(\boldsymbol{x})=f(\boldsymbol{x_{0}})+\triangledown f(\boldsymbol{x_{0}})^{T}(\boldsymbol{x}-\boldsymbol{x_{0}})+\frac{1}{2}(\boldsymbol{x}-\boldsymbol{x_{0}})^{T}H(\boldsymbol{x_{0}})(\boldsymbol{x}-\boldsymbol{x_{0}})+...$

$\triangledown f(\boldsymbol{x{0}})$是$f$在$\boldsymbol{x{0}}$处的梯度
$H(\boldsymbol{x{0}})$是$f$在$\boldsymbol{x{0}}$处的海塞矩阵

2.2 海赛矩阵判定多元函数极值

定理：设n元函数$f(x{1},x{2},…,x{n})$在点 $M{0}(a{1},a{2},…,a_{n})$的邻域内有二阶连续偏导，如果f在该点梯度为0，则可以通过该点的二阶偏导即海塞矩阵H判断函数在该点是否取得极值。

如果H为正定矩阵，函数在该点取得极小值；
如果H为负正定矩阵，函数在该点取得极大值；
如果H是半正定或半负定，该点是可疑极值点，需更通过其他方法来判定；
如果H是不定矩阵，该点不是极值点；

3. 矩阵求导

矩阵求导的技术，在统计学、控制论、机器学习等领域有广泛的应用。鉴于看过的一些资料或言之不详、或繁乱无绪，本文来做个科普，以下内容参考：

矩阵求导术（上）

矩阵求导术（下）

3.1 全导数与全微分

全导数：标量f对矩阵X的导数为f对X逐元素求导排成与X尺寸相同的矩阵

$f^{'}(X)=\begin{bmatrix} \frac{\partial f}{\partial X_{ij}} \end{bmatrix}$

对于标量：$f^{‘}(x)=\begin{bmatrix}
\frac{\partial f}{\partial x}
\end{bmatrix}=\frac{\mathrm{d} f}{\mathrm{d} x}$
对于向量：$f^{‘}(\boldsymbol{x})=\begin{bmatrix}
\frac{\partial f}{\partial x_{i}}
\end{bmatrix}=\triangledown f(\boldsymbol{x})$

全微分：全增量△f的线性主部

$df = \sum_{i,j} \frac{\partial f}{\partial X_{ij}}dX_{ij}$

对于标量：$df = \frac{\partial f}{\partial x}dx$
对于向量：$df = \sum{i} \frac{\partial f}{\partial x{i}}dx_{i}$

对于规模相同的矩阵A和B，有：

$\text{tr}(A^TB) = \sum_{i,j}A_{ij}B_{ij}$

因此，全微分等于矩阵导数与$dX$内积的迹（trace）

$df = \sum_{i,j} \frac{\partial f}{\partial X_{ij}}dX_{ij} = \text{tr}\left(f^{'}(X)^T dX\right)$

对于标量：$df = \frac{\partial f}{\partial x}dx=tr(f^{‘}(x)^Tdx)=f^{‘}(x)dx$
对于向量：$df = \sum{i} \frac{\partial f}{\partial x{i}}dx_{i}=tr(f^{‘}(\boldsymbol{x})^Td\boldsymbol{x})=tr(\triangledown f(\boldsymbol{x})^Td\boldsymbol{x})$

3.2 标量对矩阵的求导规则

3.2.1 一般思路

最重要的一点要记住：微积分中对标量求导的结论不适用于对矩阵求导！比如认为AX对X的导数为A，这是没有根据的。我们需要重新建立对矩阵求导的规则，全导数的定义在计算中并不好用，因为它需要将矩阵拆做单个元素，而使用矩阵表示函数的意义正在于矩阵运算更加简洁，因此我们希望找到一种从整体出发的算法。回想一元函数的求导，通常不是从定义出发来求极限，而是先建立初等函数求导、四则运算和复合求导的链式法则，我们也将按照这样的思路来建立对矩阵求导的运算法则。

由：

$df = \text{tr}(df) = \text{tr}\left(f^{'}(X)^T dX\right)$

可将矩阵求导分解为两个步骤：

微分化简：通过微分化简提出$dX$
迹化简：通过迹化简将$dX$移至微分右侧，则微分中$dX$左侧部分既是矩阵导数

3.2.2 矩阵微分运算法则

常矩阵：$dC=\boldsymbol{0}$，0矩阵
加减：$d(X \pm Y )=dX \pm dY$，线性$d(aX \pm C )=adX$
乘法：$d(XY) = dX Y + X dY $
转置：$d(X^T) = (dX)^T$
逆：$dX^{-1} = -X^{-1}dX X^{-1}$。此式可在$XX^{-1}=I$两侧求微分来证明
迹：$d\text{tr}(X) = \text{tr}(dX)$
行列式： $d|X| = \text{tr}(X^{*} dX)$ ，其中 $X^{*}$表示X的伴随矩阵，在X可逆时又可以写作$d|X|= |X|\text{tr}(X^{-1}dX)$
逐元素乘法：$d(X\odot Y) = dX\odot Y + X\odot dY，\odot$表示尺寸相同的矩阵X,Y逐元素相乘
逐元素函数：$d\sigma(X) = \sigma’(X)\odot dX ，\sigma(X) = \left[\sigma(X_{ij})\right]$是逐元素运算的标量函数

3.2.3 矩阵微分复合法则

对符合函数求导$f^{‘}(U(X))$，其中$U$和$X$均为矩阵，有以下微分复合法则：

$\begin{align*} df=tr(df)&=tr(f^{'}(U)^TdU)\\ &=tr(f^{'}(U)^Ttr(U^{'}(X)^TdX)) \end{align*}$

同样不能将对标量求导的复合法则搬到这里，以下公式对矩阵求导不成立：

$f^{'}(U(X))=f^{'}(U)U^{'}(X)$

3.2.4 矩阵迹运算法则

标量：$a = \text{tr}(a)$
转置：$\mathrm{tr}(A^T) = \mathrm{tr}(A)$
线性：$\text{tr}(A\pm B) = \text{tr}(A)\pm \text{tr}(B)$
矩阵乘法交换：$\text{tr}(AB) = \text{tr}(BA)$，A B规模相反，两侧都等于$\sum{i,j}A{ij}B_{ji}$，乘法交换迹不变!
矩阵乘法/逐元素乘法交换：$\text{tr}(A^T(B\odot C)) = \text{tr}((A\odot B)^TC)$，A B C规模相同，两侧都等于$\sum{i,j}A{ij}B{ij}C{ij}$

记忆：前三个通过迹的定义可直观得到，最重要的是矩阵乘法交换：

3.3 重要实例

有些资料在计算矩阵导数时，会略过求微分这一步，这是逻辑上解释不通的。

例1：【线性函数】 $f=w^TX$，求$f^{‘}(X)$

解：$df=d(w^TX)=d(w^T)X+w^TdX=w^TdX=tr(w^TdX)$，因此$f^{‘}(X)=w$

例2：$f=X^THX$

解：

$\begin{align*} df=d(X^THX)&=d(X^T)HX+X^Td(HX)\\ &=d^T(X)HX+X^T(dHX+HdX)\\ &=tr(d^T(X)HX)+tr(X^THdX)\\ &=tr(X^TH^TdX+X^THdX)\\ &=tr((X^TH^T+X^TH)dX) \end{align*}$

因此，$f^{‘}(X)=(X^TH^T+X^TH)^T=(H+H^T)X$

特殊地，当H为对称矩阵，$f^{‘}(X)=2HX$

例3：【线性回归】：$l = |X\boldsymbol{w}- \boldsymbol{y}|^2$，求$l^{‘}(w)$

解：$l = (X\boldsymbol{w}- \boldsymbol{y})^T(X\boldsymbol{w}- \boldsymbol{y})$，求微分，使用矩阵乘法、转置等法则：$dl = (Xd\boldsymbol{w})^T(X\boldsymbol{w}-\boldsymbol{y})+(X\boldsymbol{w}-\boldsymbol{y})^T(Xd\boldsymbol{w}) = 2(X\boldsymbol{w}-\boldsymbol{y})^TXd\boldsymbol{w}$。对照导数与微分的联系，得到$l^{‘}(w)= 2X^T(X\boldsymbol{w}-\boldsymbol{y})$
例4【多元logistic回归】：$l = -\boldsymbol{y}^T\log\text{softmax}(W\boldsymbol{x})，求\frac{\partial l}{\partial W}$。
例5【方差的最大似然估计】：已知样本 $ \boldsymbol{x}_1,\dots, \boldsymbol{x}_n \sim N(\boldsymbol{\mu}, \sigma) $ ，

其中 $\sigma $是对称正定矩阵，求方差 $\sigma$ 的最大似然估计。写成数学式是：$l = \log|\sigma|+\frac{1}{n}\sum_{i=1}^n(\boldsymbol{x}_i-\boldsymbol{\bar{x}})^T\sigma^{-1}(\boldsymbol{x}_i-\boldsymbol{\bar{x}})$，求$\frac{\partial l }{\partial \sigma}$的零点。
例6【二层神经网络】$l = -\boldsymbol{y}^T\log\text{softmax}(W_2\sigma(W_1\boldsymbol{x}))$，求$\frac{\partial l}{\partial W_1}$和$\frac{\partial l}{\partial W_2}$。其中$\boldsymbol{y}$是除一个元素为1外其它元素为0的向量，$\text{softmax}(\boldsymbol{a}) = \frac{\exp(\boldsymbol{a})}{\boldsymbol{1}^T\exp(\boldsymbol{a})}$同例3，$\sigma(\cdot)$是逐元素sigmoid函数$\sigma(a) = \frac{1}{1+\exp(-a)}$

神经网络的求导术是学术史上的重要成果，还有个专门的名字叫做BP算法，我相信如今很多人在初次推导BP算法时也会颇费一番脑筋，事实上使用矩阵求导术来推导并不复杂。为简化起见，我们推导二层神经网络的BP算法

略…