机器学习：理论基础（七）—— 泛化理论

机器学习的目的可以被简单概括为“寻找泛化误差最小的模型”，学习问题可以被分解为两个基本问题：

使模型的经验误差最小，这可以通过经验风险最小化来达到；
使模型的经验误差尽可能接近泛化误差，这主要受到样本容量和模型复杂度的影响。样本容量就是数据量的多少，模型复杂度可以通过假设空间的VC维来衡量；

与两个基本问题相对应，我们可以将算法的期望泛化误差分解为偏差和方差两部分。偏差-方差分解是我们在分析机器学习系统性能的影响因素、改进机器学习系统性能时所用到的最重要工具。如果我们的机器学习系统性能欠佳，要么可归因于高偏差（欠拟合）要么可归因于高方差（过拟合）。如果把构建机器学习系统比作开车，那么偏差-方差分解就是我们的仪表盘，增加方差的措施就是在踩油门，减少方差的措施就是在踩刹车，只有将车速维持在适当水平才能安全驾驶。

学习曲线描述了经验误差和泛化误差随样本容量增加的变化趋势，通过学习曲线可以识别出增加样本容量是否能够改善机器学习系统的性能。

形式化学习问题（Why can machine learn?）

监督学习

监督学习：从带标签的训练集中识别出特征到标签的某种模式g，作为理想模式的近似。

目标函数(Target Function)：$y = f(x)$是特征到标记的理想模式(未知)，$(x{i},y{i})$是数据集中的观测样例，$y{i}=f(x{i})+\zeta $，$\zeta$表示噪声；
假设函数（Hypothesis Function）：$y = h(x)$是假设空间$H={h:X \to Y | h = h(x)}$中的某个模型；
损失函数（Loss Function）：$L=L(y,h(x))$，计算样本预测值和观测值的误差；
经验误差（Training error）：在训练集上损失函数的均值

$E_{in}(h) = \frac{1}{m}\sum_{i=1}^{m}L(y_{i},h(x_{i}))$

泛化误差（Generalization error）：在测试集上损失函数的期望/均值，在做交叉验证时将验证误差作为泛化误差的近似。 $E_{out}(h) = \mathbb{E}_{(x,y)\in (x,f(x))}[L(y,h(x))]$

学习问题——经验风险最小化和结构风险最小化

经验风险最小化

经验风险最小化(empirical risk minimization,ERM)：选取经验误差最小的模型作为最终模型。

$g= \underset{h\in H}{argmin} E_{in}(h)$

泛化误差界

如果仅追求经验风险最小化，那么使用较复杂的模型，能够在样本集上轻易达到100%的正确率，但在真实分类时却一塌糊涂。

统计学习因此而引入了泛化误差界的概念，就是指真实风险应该由两部分内容刻画:

经验风险：代表了分类器在训练样本上的误差；经验风险最小化要做的只是让这部分误差达到最小；
置信风险：代表了我们在多大程度上可以信任分类器在未知样本上分类的结果；也就是经验误差在多大程度上接近泛化误差。这部分是没有办法精确计算的，只能给出一个估计的区间，使得整个泛化误差只能计算上界，无法计算准确的值（所以叫做泛化误差界，而不叫泛化误差）。

泛化误差界的公式可以简单表示如下：

$E_{out} \leqslant E_{in} + \Phi (d_{vc},n,\delta )$

$E_{out} $：泛化误差
$E_{in} $：经验风险
$\Phi (d{vc},n,\delta )$：置信风险，$n$表示训练集规模，$d{vc}$表示模型复杂度/假设空间VC维，$\delta$表示置信度。置信风险随训练集规模增大而指数级衰减，随模型VC维增加而多项式级增加，随置信度增加而减小。

结构风险最小化

结构风险最小化(Structural Risk Minimization,SRM)：选取经验风险和置信风险之和最小的模型作为最终模型。

结构风险最小化可以转化为以下两个核心问题：

经验误差是否足够小：通过经验风险最小化来达到

$g= \underset{h\in H}{argmin} E_{in}(h)$

泛化误差是否足够接近经验误差：由样本容量和模型复杂度决定

$E_{out}(g) \approx E_{in}(g)\approx 0$

VC维

VC维（Vapnik-Chervonenkis Dimension，由研究人员Vapnik和Chervonenkis在1958年发现）：对于一个指示函数集H，如果存在k个样本，它的任何一种划分($2^k$)都能够被H中的函数f分开，则称H能够把k个样本打散(shatter)，函数集的VC维就是它能打散最大样本数。

VC维反映了函数集的学习能力，VC维越大模型越复杂，相应地，函数集的学习能力越强。遗憾的是，目前尚没有通用的关于任意函数集VC维计算的理论，只对一些特殊的函数集知道其VC维。

单个假设

由霍夫丁（hoeffding）不等式:

$P[|E[X]-\overline{X}|>\epsilon ] \leqslant 2exp\left ( \frac{-2m\epsilon ^{2}}{(b-a)^2} \right )$

应用到泛化误差上，假设错误限定在0和1之间，则对于假设h有：

$P[|E_{out}(h)-E_{in}(h)|>\epsilon ]\leqslant 2exp\left ( -2m\epsilon ^{2} \right )$

结论：对于单个假设，经验误差与泛化误差间的差异随着样本容量的增长而指数级衰减

有限假设空间

由：

$P(\bigcup_{i=1}^{n}x_{i})\leqslant \sum_{i=1}^{n}P(x_{i})$

得：

$\begin{align*} P[\underset{h\in H}{sup}|E_{out}(h)-E_{in}(h)|>\epsilon ]&\leqslant \sum_{h\in H}P[|E_{out}(h)-E_{in}(h)|>\epsilon ]\\ &\leqslant 2|H|exp\left ( -2m\epsilon ^{2} \right ) \end{align*}$

结论：

但当有多个假设时会恶化算法的泛化性能；
经验误差和泛化误差的差异，随训练集样本数的增加而指数级衰减，随假设空间容量增加而增加。

无限假设空间

存在很多以实数为参数的模型，假设空间中的假设数量将是无穷的，此时根据该不等式无法给出经验误差和泛化误差的一个确定的上界。事实上，在放大不等式右侧的过程中我们假设了各个假设模型相互独立，而事实上模型之间会有很大程度的交集，也就是说它被过度放大了。我们希望能够找到一个多项式级别的函数来代替|H|用于描述假设空间的复杂度。

成长函数（Growth Function）：假设空间H中有效模型个数与样本容量m的函数关系称作该假设空间的成长函数，记做$m_{H}(m)$。H中所有将样本集划分为相同结果的模型都被看作是同一个有效模型，我们希望用假设空间中有效模型个数来代替模型总数|H|，对于样本数为m的二分类问题，其有效模型数的一个上界为$2^{m}$，但是这个指数上界仍然过于宽泛了，我们希望将其缩减到一个多项式级别的函数。

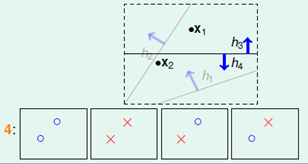
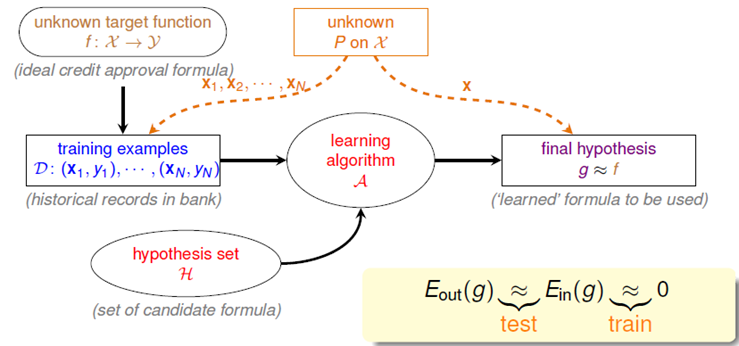
$P[\underset{h\in H}{sup}|E_{out}(h)-E_{in}(h)|>\epsilon ]\leqslant 2m_{H}(m)exp\left ( -2m\epsilon ^{2} \right )$

打散（Shatter）：对于假设空间H，如果存在k个样本，它的任意划分都可以被H中的函数分开，就说假设空间H能够shatter k个样本。二维感知机模型的VC维为3。

VC维（Vapnik-Chervonenkis Dimension）：H所能shatter的最大样本数，称该假设空间的VC维；
突破点（Break Point）：如果任意k个样本都不能被H打散，则称k为H的突破点。如果k是H的突破点则任意比k大的整数也是H的突破点，H的最小突破点=VC(H)+1；

上限函数（Bounding function）：是指当假设空间H的最小突破点为k时，H的成长函数的最大值，记做B(N,k)，上限函数满足以下不等式（假设空间的成长函数以其VC维次多项式为上限）：

$B(N,k)\leqslant B(N-1,k)+B(N-1,k-1)\\ m_{H}(N)\leqslant B(N,k)\leqslant \sum_{i=0}^{k-1}C_{N}^{i}\leqslant N^{k-1}=N^{d_{vc}}\\ m_{H}(N)\leqslant N^{d_{vc}}$

举例：

输入	假设	成长函数	VC维
一维点集	正射线	N+1	1
一维点集	正区间	$\binom{N+1}{2}+1$	2
二维点集	凸集	$2^N$	$\infty$
d维点集	N维线性分类器	$N^{d+1}$	d+1

结论：使用上限函数代替假设空间容量|H|，有以下不等式

$P[\underset{h\in H}{sup}|E_{out}(h)-E_{in}(h)|>\epsilon ]\leqslant 4N^{d_{vc}}exp\left ( -\frac{1}{8}\epsilon ^{2} N \right )$

如果假设空间VC维有限，则随着样本容量的增加，模型的经验误差趋近于泛化误差；
假设空间VC维与假设空间中自由参数的个数大致相等；

泛化误差界：通过VC维重写本文开头给出的泛化误差界

$E_{out}(g) \leqslant E_{in}(g) + \sqrt{\frac{8}{N}ln(\frac{4(2N)^{d_{vc}}}{\delta })}$

正则化

正则化：通过约束模型参数向量的范数使其不要太大，来降低模型复杂度以降低过拟合风险。

$L^∗(y_i,f(x_i;w))=L(y_i,f(x_i;w))+γΩ(w)\\ w=\underset{w}{argmin}L^*$

正则项实际上是一种惩罚机制：若增加模型复杂度所换取的在损失函数上的增益不足抵消因此导致的正则项的增加，那么增加这样的复杂度就是得不偿失的。正则化是结构最小化的等价形式。

范数

范数：在赋范空间中用于度量向量大小的函数。

范数的性质：

非负性：$ \lVert\vec x\rVert\geqslant 0 $；
齐次性：$ \lVert c\cdot\vec x\rVert = \lvert c\rvert \cdot \lVert\vec x\rVert$；
三角不等式：$ \lVert \vec x + \vec y\rVert \leqslant \lVert\vec x\rVert + \lVert\vec y\rVert$;

范数的性质使得它天然地适合作为机器学习的正则项。而范数需要的向量，则是机器学习的学习目标——参数向量。

常用范数：

$L{p}范数$：各元素绝对值的p次方和的p次方根，$ \lVert\vec x\rVert_p = \Bigl(\sum{i = 1}^{d}|x_i|^p\Bigr)^{1/p} $
$L_0$范数：向量中非零元素个数，$ \lVert\vec x\rVert_0 = x_i,\; \text{with }x_i\neq 0 $
$L{\infty }$：各元素中最大的绝对值，$ \lVert\vec x\rVert\infty = \lim{p\to+\infty}\Bigl(\sum{i = 1}^{d}x_i^p\Bigr)^{1/p} $

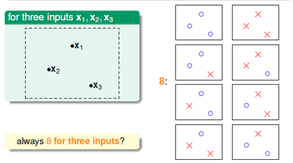
机器学习中常用的范数是L1和L2范数:

L1范数：向量中所有元素的绝对值的和，$ \lVert\vec x\rVert1 = \sum{i = 1}^{d}\lvert x_i\rvert $
L2范数：向量长度，$ \lVert\vec x\rVert2 = \Bigl(\sum{i = 1}^{d}x_i^2\Bigr)^{1/2} $

L1范数（LASSO regularizer）

损失函数后面加上L1正则项就成了著名的Lasso问题（Least Absolute Shrinkage and Selection Operator）。

L1是L0的备胎：从特征选择的角度来看，适当减少特征维度可以降低模型复杂度从而降低过拟合的风险。嵌入式特征选择就是在模型训练过程中对参数施加“稀疏性”约束，即使得参数w尽可能多的分量变为0。最直接方式就是使用L0范数，但是L0范数不连续，难以进行优化求解，L1是L0的最优凸近似，因此常使用L1范数来代替0来产生稀疏解。

$Ω(w)=||w||_1$

L1范数能够产生稀疏解。即大多数参数被优化为0，这相当于进行了特征选择，最终只有少数特征在起作用；

L2范数（Ridge Regularizer）

在损失函数（或代价函数）后面加上L2正则项就变成了岭回归（Ridge Regression），也有人叫他权重衰减。

$Ω(w)=||w||^2_2$

L2倾向于使参数稠密地接近于0。L2相对L1更平滑，L2会让每个参数都接近0但是不会等于0，每个特征都较小。

对比L1、L2正则项

相同点：都是通过约束模型参数向量的范数来降低模型复杂度，减少过拟合风险；
不同点：
1. L1也称Lasso，倾向于产生稀疏解。使较多的参数变为0，相当于做了特征选择。
2. L2也称岭回归(Ridge Reg)，倾向于使参数稠密地接近于0。每个参数都接近0但是不会等于0，防止模型overfit到某个feature上。

各种分析曲线

偏差-方差分解

偏差方差分解：模型H的期望泛化误差可以分解为模型预测值的方差与期望预测值与真实值的偏差。

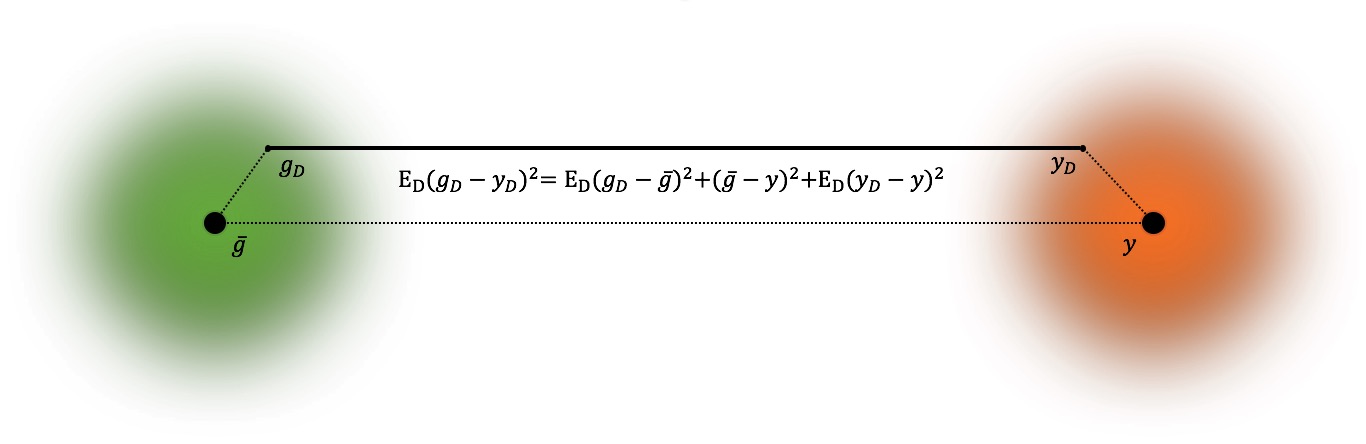
$\begin{align*} \mathbb{E}_{D}(g_{D}-y_D)^2 &= \mathbb{E}_{D}(g_{D}-\bar{g}+\bar{g}-y_D)^2 \\ &= \mathbb{E}_{D}(g_{D}-\bar{g})^2+ \mathbb{E}_{D}(\bar{g}-y_D)^2\\ &=\mathbb{E}_{D}(g_{D}-\bar{g})^2+ \mathbb{E}_{D}(\bar{g}-y+y-y_D)^2\\ &=\mathbb{E}_{D}(g_{D}-\bar{g})^2+ \mathbb{E}_{D}(\bar{g}-y)^2+\mathbb{E}_{D}(\bar{g}-y)(y-y_{D})+\mathbb{E}_{D}(y-y_{D})^2\\ &=\mathbb{E}_{D}(g_{D}-\bar{g})^2+ (\bar{g}-y)^2+\mathbb{E}_{D}(y_D-y)^2\\ &=var(x)+bias^2(x)+\epsilon^2 \end{align*}$

$g$：模型
$g_D$：样本$x$在训练集D上的预测标记
$\bar{g}$：样本$x$在不同训练集D上的期望预测标记$\bar{g}=\mathbb{E}_{D}[g_D(x)]$
$y_D$：样本$x$在训练集D中的观测标记
$y$：样本$x$的真实标记
假设噪声期望为0：$\mathbb{E}_{D}[y_D-f(x)]=0$

偏差方差分解将模型的期望泛化误差分解为三部分：

偏差：期望预测值与真实值的偏差；代表了模型本身的拟合能力；
方差：模型在不同数据集上的预测方差；代表了，即数据扰动造成的影响；
噪声：观测值与真实值的差别；代表了问题本身的误差下界；

提升泛化能力的方法：泛化性能是由算法的拟合能力、数据的充分性、任务本身的难度共同决定的（三因素：算法-数据-噪声）；给定学习任务，为获取较好的泛化能力，可以从以下三个角度来思考：

数据：保证数据数量（减少扰动）、质量（减少噪声）
算法：结构风险最小化，充分拟合数据、控制模型复杂度（减少偏差和方差）

偏差-方差窘境：学习任务的目标是要获取期望泛化误差最小的模型，也就是说让偏差和方差都尽可能小，但不幸的是偏差和方差是有冲突的：

当训练不足时，学习器的拟合能力不强，数据扰动不足以影响泛化能力，偏差主导了泛化误差，发生欠拟合；
随着训练程度的加深，学习器的拟合能力逐渐加强，数据扰动渐渐能被学习器学到
当训练程度充足后，学习器的拟合能力非常强，数据的轻微扰动都会导致学习器发生显著变化，方差主导了泛化误差。若数据自身的非全局特性被学习器学到则发生过拟合；

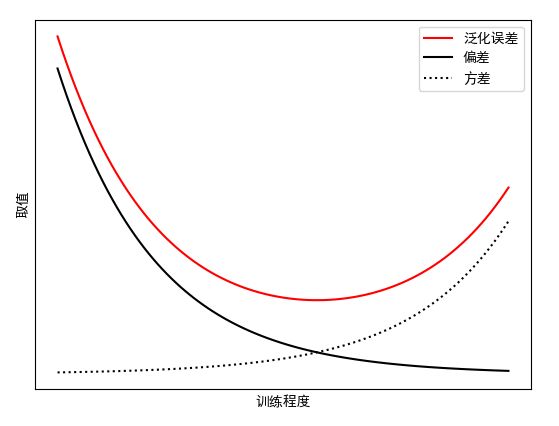
“油门曲线”横坐标可以是训练程度、模型复杂度、VC维、自由参数个数。

如果把训练模型比作开车，模型复杂度比作车速，偏差-方差曲线就是车速仪表盘，而能够增加模型复杂度的措施相当于在“踩油门”，降低模型复杂度的措施相当于在”踩刹车“，车速过快或过慢都不能保证驾驶安全。

学习曲线

学习曲线反映了经验误差和泛化误差与训练集样本数量的关系。

由经验风险最小化和VC维的相关知识可以得出学习曲线的如下结论：

当样本数较少时，如果样本数小于假设空间的VC维，模型可以将样本完全分开，此时训练误差为0，但是经验误差和泛化误差差距很大导致泛化误差很大；随着样本数的增加，模型无法将样本完全拟合，经验误差变大，同时泛化误差与经验误差的差距以接近指数级衰减；当样本数足够大时，经验误差趋于平稳，经验误差和泛化误差差距趋于0。
对于简单模型，模型的学习能力较差，经验误差和泛化误差会更早地趋于一致，但稳定后的泛化误差较高，可能发生欠拟合。此时再通过增加样本量的方法无法提高学习算法的泛化性能；
对于复杂模型，模型的学习能力很强，经验误差和泛化误差会更晚地趋于一致，稳定后的泛化误差较小，在样本数不足的时候，会发生过拟合。但是如果样本数充足，复杂模型的性能要优于简单模型；

可以把训练集规模看做是路的宽度，训练集中噪声看作是路况。路窄就要慢车速，路宽才可以飙车速；车速较低时增加路宽意义不大，车速较高时增加路宽使驾驶更安全；

正则项影响曲线对误差:

当 λ 较小时，训练集误差较小(过拟合)而交叉验证集误差较大
随着λ的增加，经验误差不断增加（欠拟合)，泛化误差先减小后增大

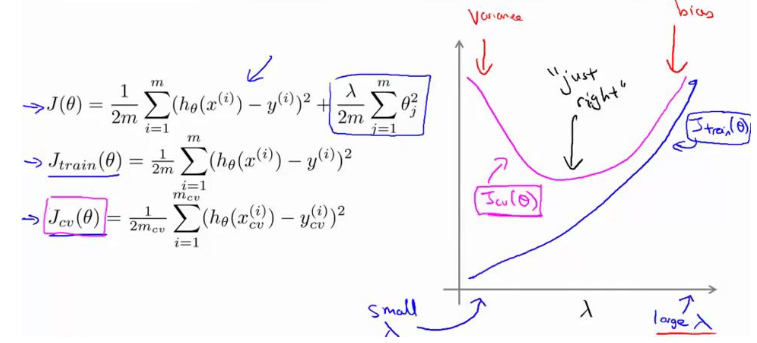
VC维和样本容量:

如果给定误差阈值$\epsilon$和精度/置信区间$\delta$（置信区间越大泛化误差可浮动的范围就越小），对$\delta$进行简化，得到$N^{d_{vc}}e^{-N}$，将其画出图像观察其变化趋势：

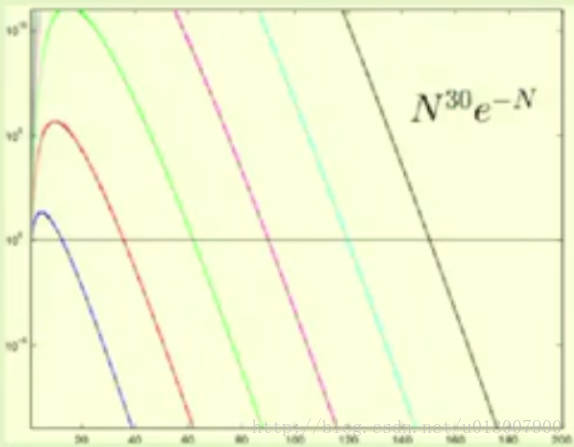
因此我们可以看到在横线所在位置，N 的增加和 dvc 几乎是一种线性的关系。经过工业界足够的现象表明，我们通常只要使得 N ≥ 10 dvc 就足够了。

提高泛化性能的方法

总体上从数据和模型两方面入手（待完善）：

数据:
1. 增加数据量
2. 增加数据质量，减少噪声
模型:
1. 使用和数据相称的模型
2. 参数惩罚

哈哈哈