机器学习：基础算法（十）—— GMM

混合模型

通过将基本的概率分布进行线性组合所得到的概率模型称为混合模型(mixture distributions)。混合模型可以用观测数据的边缘概率来描述：

$p(x)=\sum_{k=1}^{K}p(z_k=1)p(x\mid z_k=1)$

$p(z_k=1)$：z为K维的二值随机变量，采用“1-of-K”表示方法，其中有且只有一个元素$z_k=1$，其余所有元素等于0，$p(z_k=1)$表示选择第k个模型分量的先验概率
$p(x\mid z_k=1)$：第k个模型分量

混合高斯模型

混合高斯模型(Gaussian misture model)是由若干个高斯分布线性组合而成的混合模型：

$p(x)=\sum_{k=1}^{K}\pi _kN(x\mid \mu _k,\Sigma_k)$

其中：

$\left\{\begin{matrix} &p(z_k=1)=\pi _k\\ &p(x\mid z_k=1)=N(x\mid \mu _k,\Sigma_k) \end{matrix}\right.$

更一般的表示：

$\left\{\begin{matrix} &p(z)=\prod_{k=1}^{K}\pi _k^{z_k}\\ &p(x\mid z)=\prod_{k=1}^{K}N(x\mid \mu _k,\Sigma_k)^{z_k} \end{matrix}\right.$

给定x的条件下，z的后验概率可以被理解为第k个模型分量对观测值x的贡献度：

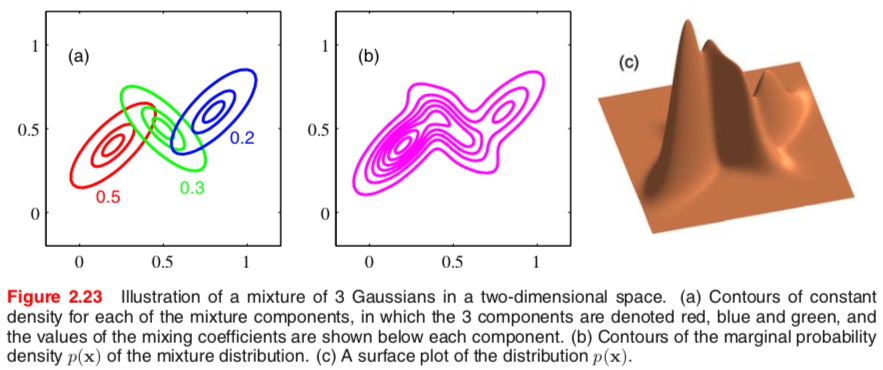
$\begin{align*} \gamma(z_k)&=p(z_k\mid x)\\ &=\frac{p(z_k=1)p(x\mid z_k=1)}{\sum_{j=1}^{K}p(z_j=1)p(x\mid z_j=1)}\\ &=\frac{\pi_kN(x\mid \mu_k,\Sigma_k)}{\sum_{j=1}^{K}\pi_kN(x\mid \mu_k,\Sigma_k)} \end{align*}$

通过使用足够多的高斯分布，通过调节它们的均值和方差以及线性组合的系数，可以以任意精度近似所有的连续概率密度分布。下图是3个高斯分布混合的例子，图a）表示三个分量的分布及混合系数，图b)表示混合分布的边缘概率分布轮廓线，图c)表示边缘分布的曲面图。

高斯混合模型的参数估计(EM算法)

可以通过极大似然估计来确定混合高斯模型中的参数：

$log\ p(X\mid \pi,\mu,\Sigma)=\sum_{i=1}^{N}log\sum_{k=1}^{K}\pi_kN(x_n\mid \mu_k,\Sigma_k)$

因为对数中存在一个求和式，导致参数的最大似然解不再有一个封闭形式的解析解。一种最大化这种似然函数的方式是使用迭代数值优化法，另一种是使用EM算法，本文接下来主要讲解EM算法。

1、明确观测变量、隐变量和参数：

将所有观测变量数据记做$X={x_1,x_2,…,x_n}$，其中$x_i$代表第i个样本
将所有隐变量数据记做$Z=[z{ik}]{n\times k}$，其中$z_{ik}=1$代表第i个样本来自第k个分模型
参数记做$\theta=(\pi,\mu,\Sigma)$，其中$\pi,\mu,\Sigma$均为K维向量，分别表示选取第k个模型的概率，第k个模型的均值和协方差

2、E步：计算完全数据的对数似然关于隐变量的条件期望函数（Q函数）

$Q(\theta,\theta^i)=\mathbb{E}_Z[log\ p(X,Z\mid \theta)\mid X,\theta^i]$

其中，完全数据的对数似然函数为：

$\begin{align*} log\ p(X,Z\mid \theta)&=log\ \prod_{j=1}^{N}p(x_j,z_j\mid \theta)\\ &=log\ \prod_{j=1}^{N}p(z_j\mid \theta)p(x_j\mid z_j,\theta)\\ &=log\ \prod_{j=1}^{N}\prod_{k=1}^{K}\pi_k^{z_{jk}}N(x_j\mid \mu_k,\Sigma_k)^{z_{jk}}\\ &=\sum_{j=1}^{N}\sum_{k=1}^{K}z_{jk}(log\pi_k+logN(x_j\mid \mu_k,\Sigma_k)) \end{align*}$

关于隐变量的条件期望：

$\mathbb{E}_Z[log\ p(X,Z\mid \theta)\mid X,\theta^i]=\sum_{j=1}^{N}\sum_{k=1}^{K}\mathbb{E}_Z(z_{jk}\mid X,\theta^i)(log\pi_k+logN(x_j\mid \mu_k,\Sigma_k))$

其中：

$\mathbb{E}_Z(z_{jk}\mid X,\theta^i)=p(z_{jk}=1\mid x_j,\theta^i)=\gamma (z_{jk})$

综上，可以写出Q函数的最终表达式:

$Q(\theta,\theta^i)=\sum_{j=1}^{N}\sum_{k=1}^{K}\gamma (z_{jk})(log\pi_k+logN(x_j\mid \mu_k,\Sigma_k))$

3、M步：关于$\theta$最大化Q函数，求出最佳参数更新$\theta$

$\theta^{i+1}=arg\ \underset{\theta}{max}\ Q(\theta,\theta^i)$

偏导等于0，可得：

(1) 第k个模型分量的混合系数等于第k个模型对所有样本的平均贡献度($N_k$代表被分到第k个分量的样本数)：

$\pi_k^{i+1}=\frac{\sum_{j=1}^{N}\gamma (z_{jk})}{N}=\frac{N_k}{N},k=1,2,...,K$

（2）第k个模型分量的均值等于所有样本关于模型贡献度的均值：

$\mu_k^{i+1}=\frac{\sum_{j=1}^{N}\gamma (z_{jk})x_j}{N_k},k=1,2,...,K$

（3）第k个模型分量的协方差等于所有样本关于模型贡献度的协方差：

$\Sigma_k^{i+1}=\frac{\sum_{j=1}^{N}\gamma (z_{jk})(x_j-\mu_k^{i+1})(x_j-\mu_k^{i+1})^T}{N_k},k=1,2,...,K$

高斯混合模型EM算法框架:

输入：观察变量数据，高斯混合模型

输出：高斯混合模型参数

（1）选取合适的参数初值，$\pi^0,\mu^0,\Sigma^0$，置i=0
（2）迭代E步和M步，直至收敛

E步：基于模型当前参数值，计算每个分模型对各个观测数据的贡献度/后验概率$\gamma (z_{jk})$，得到Q函数
M步：最大化Q函数，更新参数