机器学习：基础算法（九）—— EM

EM(expectation maximization)算法是一种迭代算法，用于含隐变量的概率模型参数的极大似然估计或极大后验概率估计。

EM算法的推导

考虑一个概率模型，将所有观测变量记做X，将所有隐变量记做Z，完全变量的联合概率分布$p(X,Z\mid\theta)$由一组参数控制，记做$\theta$。我们的目标是通过观测变量的极大似然来估计最优参数$\theta^*$

$$\theta^*=\underset{\theta}{max}\ log\ p(X\mid\theta)=\underset{\theta}{max}\ log\ \sum_{Z}p(X,Z\mid\theta)$$

因为对数中包含了联合概率分布的和(或积分)，直接最优化$log\ p(X\mid\theta)$比较困难，通过引入隐变量分布$q(Z)$，可以将观测变量的对数似然分解为一个下界加上$q(z)$与$p(Z|X,\theta)$的KL散度(代入可证)：

$$L(\theta)=logp(X|\theta)=B(q,\theta)+KL(q||p)$$

其中：

$$\left\{\begin{matrix} &B(q,\theta)=\sum_{Z}q(Z)log\frac{p(X,Z|\theta)}{q(Z)}\\ &KL(q||p)=-\sum_{Z}q(Z)log\frac{p(Z|X,\theta)}{q(Z)} \end{matrix}\right.$$

KL散度总是大于等于0，故$B(q,\theta)$是$L(\theta)$的一个下界：

$$L(\theta)\geqslant B(q,\theta)$$

EM算法是一个两阶段的迭代算法，通过不断提升对数似然函数的下界来搜索对数似然函数的极大值。假设参数当前值为$\theta_k$，可以用以上似然分解来定义这两个阶段：

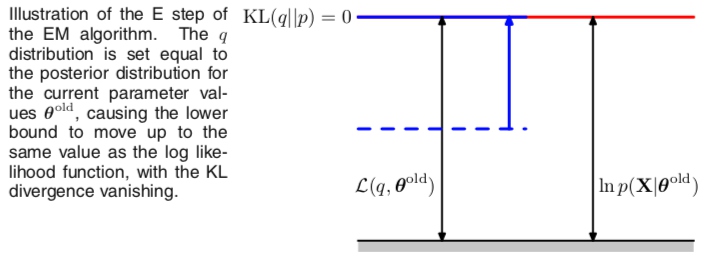
1、 E步：固定当前参数$\theta_k$，关于隐变量分布$q(Z)$最大化下界函数$B(q,\theta_k)$，逼近当前的对数似然函数值。很明显下界函数的最大值出现在$q(z)$与$p(Z|X,\theta)$的KL散度为0的时候，即$p(Z|X,\theta_k)=q(Z)$。

此时下界函数可表示为：

$$\begin{align*} B(q,\theta)&=\sum_{Z}p(Z|X,\theta_k)logp(X,Z|\theta)-\sum_{Z}p(Z|X,\theta_k)logp(Z|X,\theta_k)\\ &=Q(\theta,\theta_k) + H_{X,\theta_k}(Z) \end{align*}$$

• $H_{X,\theta_k}(Z)$：分布q(Z)的熵，为常数，与$\theta$无关；
• $Q(\theta,\theta_k)$：Q函数，完全数据的对数似然关于隐变量分布的期望；

此时下界函数值等于对数似然函数值：

$$\begin{align*} B(q,\theta_k)&=\sum_{Z}p(Z|X,\theta_k)logp(X,Z|\theta_k)-\sum_{Z}p(Z|X,\theta_k)logp(Z|X,\theta_k)\\ &=\sum_{Z}p(Z|X,\theta_k)logp(X|\theta_k)\\ &=logp(X|\theta_k)\\ &=L(\theta_k) \end{align*}$$

E步的几何解释：q分布被置为当前参数下的后验概率分布，使得KL散度为0，下界函数上移到与观测数据对数似然相等的位置。

2、M步：固定当前隐变量分布，关于参数$\theta$最大化下界函数$B(q,\thetak)$，得到某个新的$\theta{k+1}$。这会增大$B(q,\thetak)$(除非已经到达极大值)，同时因为概率分布q由$\theta_k$确定，并在M步保持不变，因此它不会等于新的后验概率分布$p(Z|X,\theta{k+1})$，从而KL散度不为0，所以对数似然的增加量大于下界函数的增加量。

$$\theta_{k+1}= arg\ \underset{\theta}{max}\ B(q,\theta)=arg\ \underset{\theta}{max}\ Q(\theta,\theta_k)$$ $$L(\theta_k)>B(q,\theta_k)$$

M步几何解释：下界函数关于参数最大化，得到修正的$\theta$，因为KL散度非负，使得对数似然函数增量至少与下界函数增量相等。

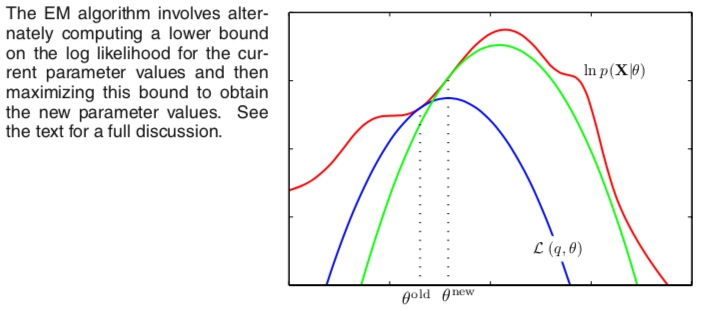
EM算法也可以看做是参数空间中的迭代：红色曲线表示观测数据对数似然函数，我们希望搜索它的极大值，首先选取某个初始参数值$\theta^{old}$，通过E步计算隐变量上的后验概率分布，关于隐变量上的后验概率分布最大化下界函数(蓝色曲线表示)，使得在$\theta^{old}$处下界函数值等于对数似然值；在M步，关于参数$\theta$最大化下界函数，得到新的$\theta^{new}$，在新参数值下对数似然值增长量大于下界函数增长量；接下来的E步又构建了一个新的下界函数(绿色)，直至对数似然函数达到极值(EM之只能达到局部最优)。

EM算法的基本框架：

输入：观测变量数据X，隐变量数据Z，完全数据联合分布$p(X,Z|\theta)$，条件分布$p(Z|Y,\theta)$，精度$\epsilon$
输出：模型参数$\theta$
（1）选择参数初值$\theta0$，置k=0
（2）如果$\left | \theta{k+1}-\theta_k \right |<\epsilon $

• E步：记$\theta_k$为第k次迭代参数的估计值，计算Q函数：

$$Q(\theta,\theta_k)=\mathbb{E}_Z[logp(X,Z|\theta)\mid X,\theta_k]=\sum_{Z}p(Z|X,\theta_k)logp(X,Z|\theta)$$

• M步：极大化Q函数，更新参数

$$\theta_{k+1}=arg\ \underset{\theta}{max}\ Q(\theta,\theta_k)$$

EM算法的收敛性

定理1：假设$\theta_k,k=1,2…$是EM算法得到的参数估计序列，则对应的对数似然函数序列是递增的。

$$L(\theta_{k+1})\geqslant B(q,\theta_{k+1})\geqslant B(q,\theta_k)= L(\theta_k)$$

定理2：如果EM的对数似然函数有上界，则EM算法得到的对数似然函数序列会收敛到某个值。

定理3：在Q函数和对数似然满足一定条件下，EM算法得到的参数估计序列会收敛到对数似然函数序列的稳定点，但不能保证收敛到全局/局部极大值点。

EM算法对初值比较敏感，在实际应用中通常选取几个不同的初值进行迭代，然后对各个估计值加以比较，从中选择最好的

EM算法用于极大后验概率估计

我们也可以使用EM算法来最大化模型的后验概率分布$p(\theta\mid X)$，其中我们已经引入了参数上的先验概率分布$p(\theta)$，我们的目标是极大化以下对数后验概率：

$$\begin{align*} log\ p(\theta\mid X)&=log\ \frac{p(\theta)p(X\mid \theta)}{p(X)}\\ &=log\ p(X\mid \theta) + log\ p(\theta)-log\ p(X)\\ &=B(q,\theta)+KL(q||p)+ log\ p(\theta)-log\ p(X)\\ &\geqslant B(q,\theta)+ log\ p(\theta)-log\ p(X) \end{align*}$$

其中$log\ p(X)$是一个常数，与之前一样，我们可以交替地关于q和$\theta$对右侧进行优化：

1. E步：因为q只出现在下界函数中，与标准EM中的E步完全相同
2. M步：通过引入先验分布$p(\theta)$进行修改，通常只需要做很小改动即可

GEM算法

EM算法将最大化似然函数这一困难问题分解为两个阶段，每个步骤一般都很容易解决，但对于复杂的模型来说，E步或M步仍然无法计算。推广的EM算法(generalized EM,GEM)解决的是M步骤无法计算的问题。

F函数的极大极大算法

EM算法还可以解释为F函数的极大极大算法：

F函数：

$$F(\tilde{P},\theta)=E_P[log\ P(X,Z\mid \theta)]+H(\tilde{P})$$

• $\tilde{P}(Z)$：隐变量数据的概率分布
• $H(\tilde{P}$：分布$\tilde{P}$的熵

E步：对固定的$\theta^i$，求$\tilde{P}^{i+1}$使$F(\tilde{P},\theta^i)$极大化

M步：对固定的$\tilde{P}^{i+1}$，求$\theta^{i+1}$使$F(\tilde{P}^{i+1},\theta)$

由EM算法和F函数的极大极大算法得到的参数估计序列是一致的。

GEM算法框架

当参数个数d大于等于2时，可采用一种特殊的GEM算法，它将EM算法的M步分解为d次条件极大化，每次只改变参数向量中的一个分量，其余分量不变。

EM评价和应用

EM算法的优缺点:

1. 优点:简单、普适
2. 缺点:收敛速度慢，只能收敛到稳定点，不能保证收敛到全局/局部最优解

EM算法的应用:

1. EM用于生成模型的非监督学习：可以认为非监督学习训练数据是联合概率分布$p(X,Y)$生成的数据，X为观测变量数据，Y为隐变量数据。
   1. K-means聚类
   2. GMM混合高斯
   3. HMM隐马尔科夫
2. 填充缺失值