机器学习：基础算法（八）—— PCA

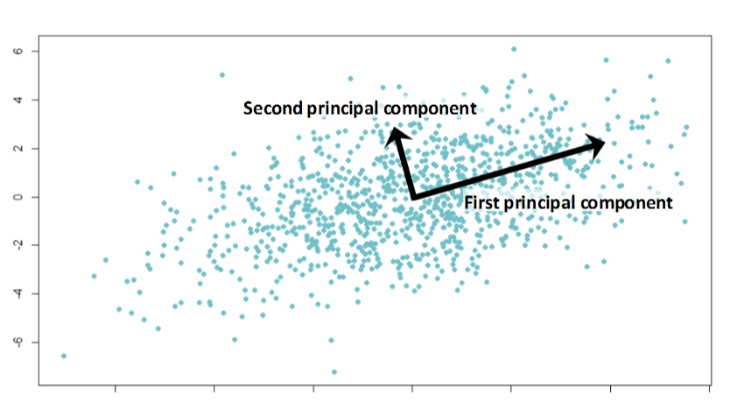
主成分分析（principal components analysis，PCA）是一种常用的降维方法，它将原始高维特征空间中的样本通过线性变换“投影”到低维特征空间，每个新的特征都是原始特征的线性组合且相互独立。

求解投影矩阵：

1. 数据样本中心化$\sum_{i=1}^{n} x_i=0$
2. 对协方差矩阵$XX^T$进行特征值分解（或奇异值分解），求出所有特征值从大到小排序
3. 取前k大特征值所对应的特征向量作为投影举证的列向量

PCA可以看做是一种数据压缩方法，主要有以下两方面的作用:

1. 降维：在损失较少信息的前提下，降低了特征空间的维度，可以降低计算量、减少特征冗余和噪声，降低过拟合的风险（吴恩达说PCA不可用来作为降低过拟合）；
2. 消除特征相关性：各主成分间相互独立，更加容易做特征选择；

基本概念

• 协方差(Covariance)：协方差用于衡量两个变量的总体误差，方差是协方差的特殊情况。两个变量的协方差等于他们乘积的期望减去期望的乘积

$$\begin{align*} cov(X,Y)&=E((X-E(x)(Y-E(Y))\\ &=E(XY)-E(X)E(Y) \end{align*}$$

• 协方差矩阵：当有多个变量时，可以使用协方差矩阵来衡量任两个变量之间的总体误差，协方差矩阵的对角线为对应变量的方差

• 空间转换：$\boldsymbol{\alpha}= [\alpha {1},\alpha {2},…,\alpha {n}]$ 和 $\boldsymbol{\beta} = [\beta {1},\beta {2},…,\beta {d}]$分别是阿尔法空间和贝塔空间的一组标准正交基，且$\boldsymbol{\beta} = \boldsymbol{\alpha}W$，W称为从阿尔法空间到贝塔空间的过度矩阵：
  • $W^TW{n\times d}=I{d\times d}$
  • 贝塔空间向量在阿尔法空间中的投影$x{\alpha } = Wz{\beta }$
  • 阿尔法空间向量在贝塔空间中的投影$z{\beta }=W^Tx{\alpha }$
• 迹运算：
  • $tr(a)=a$
  • $tr(A)=tr(A^T)$
  • $\text{tr}(A\pm B) = \text{tr}(A)\pm \text{tr}(B)$
  • $tr(AB)=tr(BA)$

PCA理论基础

PCA主要解决的问题是：如何寻找一个超平面，使得样本在该超平面内的投影能够尽可能多的保留数据集中的有用信息，PCA两种等价的推导方式：

1. 最大投影方差：样本点在超平面的投影方差最大
2. 最小投影距离：样本点到超平面的距离和最小

最大投影方差

方差和熵都是通过描述不确定性的多少来量化信息的，PCA希望投影后尽可能保留原始数据中的信息，可以通过最大化投影后的样本方差来实现。在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，信噪比越大越好。

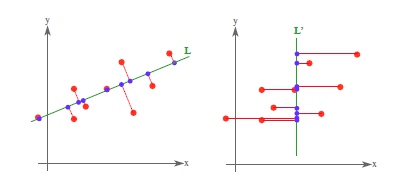
1）特征空间的转置：$X = [x{ij}]{m\times n}=[\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n]$，列向量$\boldsymbol{x}_i$代表了第i个样本（因为投影矩阵是对列向量进行投影）

2) 数据集去中心化：$\boldsymbol{x}_{i}\leftarrow \boldsymbol{x}_{i}-\bar{x}$，去中心化之后$XX^T$即代表了各个特征的协方差矩阵

3) 投影矩阵：$W=[w{1},w{2},…,w{k}]\{m\times k}$，其中$w{i}$是m维空间中的标准正交基，$ W^TW=I\{k\times k} $

4) 投影：$x{i}$在k维空间中的投影可以表示为：$W^Tx{i}$

5) 投影方差：

$$\begin{align*} V &= \sum_{i=1}^{n}\left \| W^Tx_{i}-\frac{1}{n}\sum_{i=1}^{m}W^Tx_{i} \right \|^2\\ &=\sum_{i=1}^{n}\left \| W^Tx_{i}\right \|^2 \\ &= \sum_{i=1}^{n} ( W^Tx_{i})^TW^Tx_{i}\\ &=\sum_{i=1}^{n}tr( ( W^Tx_{i})^TW^Tx_{i})\\ &=\sum_{i=1}^{n}tr( W^Tx_{i}( W^Tx_{i})^T)\\ &=\sum_{i=1}^{n}tr(W^Tx_{i}x_{i}^TW)\\ &=tr(W^T(\sum_{i=1}^{n}x_{i}x_{i}^T)W)\\ &=tr(W^TXX^TW)\\ &=tr(\Lambda) \end{align*}$$

6) 投影方差最大优化问题：$XX^T$为正定矩阵，$W$为正交矩阵，只需要求出特征协方差矩阵 $XX^T$ 的前k大的特征值 $(\lambda{1},\lambda{2},…\lambda{k})$ 及其对应的特征向量 $(w{1},w{2},…w{k})$；

$$\begin{align*} \underset{W}{max}& \text{ tr}(W^TXX^TW)\\ s.t. & W^{T} W=I \end{align*}$$

7） k维的投影超平面:$W = (w{1},w{2},…w_{k})$

8） 投影方差为$\sum{i=1}^{k}\lambda {i}$

9） 重构阈值：PCA降维后的维数k通常由用户事先指定，也可以从重构角度设置一个重构阈值来代表降维后信息保留的比例（一般要求90%以上）：

$$\frac{\sum\_{i=1}^{k}\lambda \_{i}}{\sum_{i=1}^{n}\lambda _{i}}\geqslant t$$

10) 将新样本投影至低维空间：中心化→投影$x{i}\leftarrow W^T(x{i}-\bar{x} )$

最小投影距离

1) 投影向量：$x{i}$在超平面W中的投影向量可以表示为$WW^Tx{i}$

2) 原样本点与基于投影重构的样本点之间的距离平方和为：

$$\begin{align*} D&=\sum_{i=1}^{n}\left \| WW^Tx_{i}-x_{i} \right \|^2\\ &= \sum_{i=1}^{n}(WW^Tx_{i}-x_{i})^T(WW^Tx_{i}-x_{i})\\ &=\sum_{i=1}^{n}(x_{i}^TWW^TWW^Tx_{i}-x_{i}^TWW^Tx_{i}-x_{i}^TWW^Tx_{i}+x_{i}^Tx_{i})\\ &=-\sum_{i=1}^{n}(x_{i}^TWW^Tx_{i})+ \text{const}\\ &=-\sum_{i=1}^{n}tr(x_{i}^TWW^Tx_{i})+ \text{const}\\ &=-\sum_{i=1}^{n}tr(W^Tx_{i}x_{i}^TW)+ \text{const}\\ &=-tr(W^TXX^TW)+ \text{const} \end{align*}$$

3) 求最小投影距离与求最大投影方差问题等价。

PCA计算过程

---

输入：样本集$D=\{\boldsymbol{x}_{1},\boldsymbol{x}_{2},…,\boldsymbol{x}_{n}\}$，低维空间维数k

输出：新的特征空间

过程:

1. 对所有样本进行中心化：$ \boldsymbol{x}_{i}\leftarrow \boldsymbol{x}_{i}-\frac{1}{m}\sum_{i=1}^{m}\boldsymbol{x}_{i}$，$X = [\boldsymbol{x}_{1},\boldsymbol{x}_{2},…,\boldsymbol{x}_{m}]$
2. 计算特征的协方差矩阵：$XX^T$
3. 对样本协方差矩阵进行特征值分解；
4. 取前k个最大的特征值所对应的特征向量组成投影矩阵：$W=[w{1},w{2},…,w_{k}]$
5. 投影：$x{i}\leftarrow W^T(x{i}-\bar{x} )$

---

核主成分分析（KPCA）：普通PCA是一种线性映射，有时需要非线性映射才能找到恰当的低维嵌入，常用方法是基于“核技巧”对线性降维方法进行“核化”

参考

主成分分析（Principal components analysis）-最大方差解释
主成分分析（Principal components analysis）-最小平方误差解释