数据结构与算法：图（四）—— 最小生成树与最短路径

理论篇

本文用到的实例：

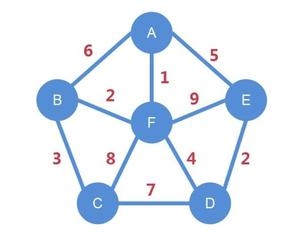
对节点进行编码，定义图的数据结构：

V_node = ['A','B','C','D','E','F']
V = range(6)
G = {0:{1:6,4:5,5:1},1:{0:6,2:3,5:2},2:{1:3,3:7,5:8},
     3:{2:7,4:2,5:4},4:{3:2,0:5,5:9},5:{0:1,1:2,2:8,3:4,4:9}}

最小生成树

连通图的最小生成树：边的权值最小的生成树，最小生成树不唯一，但最小生成树中权值之和唯一。

求解最小生成树的算法依赖于如下性质：如果U是V的一个子集，且(u,v)是连接U与V-U的最小权值边，则必存在一棵包含(u,v)的最小生成树。

Prim算法——双边袋法

• 问题：给定连通图G，找到一棵最小生成树
• 思路：prim算法和Dijkstra算法非常类似，同样可以用双袋法求解，不同之处在于这里的袋子存放的是边：
  • 树边袋：存储的是已纳入最小生成树的边
  • 图边袋：存储的是剩余顶点到树袋中所有顶点的最小边的权值
  • 更新规则：每次从图袋中选取一个最小边(u,v)，移至图袋，用该边的尾部节点更新图袋

输入：邻接表示的图G，列表表示的顶点V
输出：最小生成树
1. 初始化两个袋子：
    1. 树边袋：初始化为空
    2. 图边袋：随机选取一个顶点，其余顶点与该顶点有边则记图边长度为权值，否则记图边长度为无穷
2. 移袋-更新：每次从图袋中选取一个边长最小的边(u,v)，移至树边袋，用顶点v更新图边袋中剩余的边(x,y)，如果d[v][y] < d[x][y]，则用边(v,y)代替边(x,y)
3. 当图边袋为空时，结束迭代，树边袋即为所求最小生成树

• 代码：为优化查找更新效率，图边袋用(u,v,w)的倒查表实现{v:(u,w)}

def Prim(G,V):
    # 1. 初始化树边袋和图边袋
    t_bag = {}
    g_bag = {v:(V[0],G[V[0]][v] if v in G[V[0]] else float('inf')) for v in V if v != V[0]}
    
    # 2. 移动-更新
    while g_bag:
        min_w = float('inf')
        u,v = (None,None)
        for y,(x,w) in g_bag.items():
            if w <= min_w:
                min_w = w
                u,v = x,y
        
        t_bag[(u,v)] = min_w
        del g_bag[v]
        
        for vv,w in G[v].items():
            if vv in g_bag and w < g_bag[vv][-1]:
                g_bag[vv] = (v,w)
        
    return t_bag  
       
Prim(G,V)
{(0, 5): 1, (1, 2): 3, (3, 4): 2, (5, 1): 2, (5, 3): 4}

• 分析：
  • 时间复杂度：$O(V^2)$，与边无关，适用于稠密图
  • 空间复杂度：$O(V)$

最短路径

• BFS：用于求解无权图的单源最短路径
• Dijkstra：用于求解非负权图的单源最短路径(无权图可以看做是一种权值为1的特例)
• Floyd：求解有权图中任意两个顶点间的最短路径

最短路径的重要性质：两点之间的最短路径也包含了路径上其他顶点间的最短路径。

BFS——逐层遍历，记录层数

BFS用于求解无权图的单源最短路径，详情参见BFS。

Dijkstra——双点袋法，移动更新

• 问题：给定一个各边权值皆为非负数的图，求源顶点到图中各个顶点的最短路径；
• 思路：Dijkstra算法可以简单通过“双点袋法”来实现：

输入：邻接表示的图G，列表表示的顶点V，源节点s
输出：源顶点s到各顶点的最短路径，各顶点在最短路径中的父节点
1. 初始化两个袋子和父亲字典：
    1. 树点袋：装有已求出顶点的最短路径长度。初始时只含源节点的最短路径长度为0
    2. 图点袋：装有剩余顶点的当前路径长度。初始时包含除源节点外的所有顶点到源节点的当前路径长度，如果为源节点的邻接点，最短路径为对应边的权值，否则即为无穷
    3. 父亲字典：初始时假设所有顶点的父节点均为源节点(和图袋中当前路径对应)
2. 移袋-更新：每次从图袋中选取当前路径长度最小的顶点u移动至树袋，并用该节点更新图袋中剩余顶点的当前最短路径。更新规则为，如果该节点的邻接点v在图袋中，且源节点通过u到达v的路径更短d[u]+d[u][v]<d[v]，则用这条更短的路径长度更新图袋中现有的源节点到顶点v的路径长度，同时更新v的父节点为u
3. 直至图点袋为空时，结束迭代，此时树袋中保存了源节点到所有顶点的最短路径长度，同时父亲字典描述了一棵“单源最短路径生成树”，注意“单源最短路径生成树”并不是“最小生成树”(V：1，2，3，4，E：(1,2)=3，(2,4)=4，(1,3)=1，(3,4)=5，从1出发得到最短路径生成树是{(1,2)，(1,3)，(3,4)}，但最小生成树是{(1,2)，(1,3)，(2,4)})

• 代码：

def Dijkstra(G, V, s):
    """
    @G:图的邻接表示,{u:{v:w,...},...}
    @V:顶点集
    @s:原顶点
    @return:所有节点的单源最短路径，父亲字典
    """
    # 1. 初始化双袋和父亲字典
    n = len(V)
    t_bag = {s:0}
    g_bag = {v:(G[s][v] if v in G[s] else float('inf')) for v in V if v != s}
    father = {v:s for v in V}
    # 2. 移袋-更新
    while g_bag:
        min_v = None
        min_w = float('inf')
        for v, w in g_bag.items():
            if w <= min_w:
                min_v, min_w = v, w
        
        t_bag[min_v] = g_bag.pop(min_v)
        
        for vv, ww in G[min_v].items():
            if vv in g_bag and min_w + ww < g_bag[vv]:
                g_bag[vv] = min_w + ww
                father[vv] = min_v
    
    return t_bag,father

Dijkstra(G,V,0)
({0: 0, 1: 3, 2: 6, 3: 5, 4: 5, 5: 1}, 
 {0: 0, 1: 5, 2: 1, 3: 5, 4: 0, 5: 0})

• 分析：
  • 适用条件：权值非负的有向图或无向图
  • 时间复杂度：$O(V^2)$
  • 空间复杂度：$O(V)$

Dijkstra算法是本文最重要的算法，因为：

1. 如果各边权值为1，则Dijkstra算法可以代替BFS求解无权图的单源最短路径问题;
2. 只需对Dijkstra算法稍加修改，就变成了求解最小生成树的Prime算法；
3. 对每个顶点应用Dijkstra算法，可以得到任意两个顶点间的最短距离，时间复杂度同样为$O(V^3)$;

Floyd——n 次绕行，更新矩阵

• 问题：给定一个不包含含有负权值回路的图，求任意两个顶点间的最短路径长度
• 思路：矩阵绕行各个顶点

输入：图G，顶点V
输出：各顶点间最短路径长度的矩阵M
1. 初始化距离矩阵M：如果uv之间有边，M[u][v]=w，否则M[u][v]=无穷
2. n次绕行更新M：迭代n次，每次M中任意两个顶点u,v通过绕行k顶点(k=0~n-1)更新M[u][v]，M[u][v]=min(M[u][v],M[u][k]+M[k][v])
3. 返回最终的M

• 代码：

def Floyd(G,V):
    """
    @G:邻接表{i:{j:w,...},...}
    @V:邻接点
    @return:最短距离矩阵
    """
    
    # 初始化M
    n = len(V)
    inf = float('inf')
    M = [[inf] * n for _ in xrange(n)]
    for i in xrange(n):
        for j in xrange(n):
            if i == j:
                M[i][j] = 0
            elif i in G and j in G[i]:
                M[i][j] = G[i][j]
    # 绕行更新M
    for k in xrange(n):
        for i in xrange(n):
            for j in xrange(n):
                M[i][j] = min(M[i][j], M[i][k] + M[k][j])
    
    return M

Floyd(G,V)
[[0, 3, 6, 5, 5, 1],
 [3, 0, 3, 6, 8, 2],
 [6, 3, 0, 7, 9, 5],
 [5, 6, 7, 0, 2, 4],
 [5, 8, 9, 2, 0, 6],
 [1, 2, 5, 4, 6, 0]]
 # 第一行与Dijkstra求出的单源最短路径是一致的

• 分析：
  • 使用条件：允许图中有负权值，但不允许含含有负权值回路
  • 时间复杂度:$O(V^3)$
  • 空间复杂度：$O(V^2)$

实战篇

[LeetCode 743. 网络延迟时间]

• 问题：

有 N 个网络节点，标记为 1 到 N。

给定一个列表 times，表示信号经过有向边的传递时间。 times[i] = (u, v, w)，其中 u 是源节点，v 是目标节点， w 是一个信号从源节点传递到目标节点的时间。

现在，我们向当前的节点 K 发送了一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1。

注意:

N 的范围在 [1, 100] 之间。
K 的范围在 [1, N] 之间。
times 的长度在 [1, 6000] 之间。
所有的边 times[i] = (u, v, w) 都有 1 <= u, v <= N 且 1 <= w <= 100。

• 代码：

def networkDelayTime(self, times, N, K):
    """
    :type times: List[List[int]]
    :type N: int
    :type K: int
    :rtype: int
    """
    # 将边表转化为邻接表
    adj = collections.defaultdict(dict)
    for u,v,w in times:
        adj[u][v] = w
    # 双袋法
    # 1. 初始化：初始化两个袋子，树袋装有已求出单源最短路径的顶点，图袋装有剩余顶点
    t_bag = {}
    g_bag = {}
    father = {}
    count = 0
    for i in xrange(1,N+1):
        if i == K:
            t_bag[i] = 0
            father[i] = None
            count += 1
        elif i in adj[K]:
            g_bag[i] = adj[K][i]
            father[i] = K
        else:
            g_bag[i] = float('inf')
            father[i] = K
    
    # 2. 移袋更新：每次从图袋中选取一个单源距离最小的顶点放入树袋，并用该顶点更新图袋中所有剩余顶点的单源距离
    while count < N:
        min_v = None
        min_w = float('inf')
        for v, w in g_bag.items():
            if w <= min_w:
                min_w = w
                min_v = v
        
        t_bag[min_v] = g_bag.pop(min_v)
        count += 1

        for vv, ww in adj[min_v].items():
            if vv in g_bag and min_w + ww < g_bag[vv]:
                g_bag[vv] = min_w + ww
                father[vv] = min_v
    
    res = max(t_bag.values())
    return res if res != float('inf') else -1