数据结构与算法：图（五）—— 欧拉路径

发表于 | 更新于: | 分类于 | 阅读次数:
字数统计: 1.4k | 阅读时长 ≈ 5

术语

  • 欧拉路径(Eulerian trail)：图中恰好将所有边都访问一次的路径；
  • 欧拉回路(Eulerian cycle)：开始节点和结束节点相同的欧拉路径，也称欧拉环；
  • 欧拉图：具有欧拉回路的图；
  • 半欧拉图：有欧拉路径但没有欧拉环的图；

存在性定理（度判定）

对于无向图：奇度个数为0或2！！

  1. 欧拉图的充要条件：奇度节点个数为0；
  2. 半欧拉图的充要条件：奇度节点个数为2；
  3. 存在欧拉路径的充要条件：奇度节点个数为0或2；

对于有向图：出入度相等或各有一个为+1和-1！！(假设出度记为正，入度记为负，出度入度和记做节点的度)

  1. 欧拉图的充要条件：所有节点出度等于入度，即所有节点度为0；
  2. 半欧拉图的充要条件：存在一个节点度为1，另一个节点度为-1，其余节点度为0；
  3. 存在欧拉路径的充要条件：所有节点度为0，或者只有两个节点不为0，且其中一个节点度为1另一个节点度为-1；

获取欧拉路径

  • 问题：判断给定图中是否存在欧拉路径，如果存在则返回其中一条欧拉路径
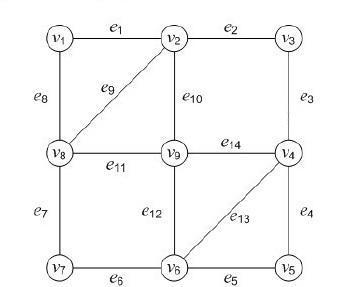
  • 分析：获取欧拉路径的一般思路：
  1. 根据存在性条件判断图中是否存在欧拉路径，并获取遍历入口；
    1. 如果是欧拉图，遍历可以从任意节点出发；
    2. 如果是半欧拉图，遍历必须从例外的两个节点出发；
  2. 调用以下算法，返回欧拉路径

Fleury算法：

算法思想：$v0$为遍历起点，令$P_0=v_0$；设$P_i=v_0e_1v_1e_2…e_i$ $v_i$已经访问，按下面方法从中选取$e{i+1}$：

1）$e{i+1}$与$v_i$相关联；
2）只有当无别的边可供访问时，才可以选择Gi=G-{e1,e2, …, ei}中的桥（所谓桥是一条删除后使连通图不再连通的边）作为$e{i+1}$；
3）当（2）不能再进行时，算法停止；

解释：我们使用栈来存储当前行走中的路径，假设当前栈顶为[…,u,v]，如果栈顶节点v还有未访问的边，我们就选择其中一条边的顶点w进行深度遍历并将遍历到的顶点压入栈中，同时删除经过的边，如果栈顶节点v所有边都已被访问，说明v的后续分量中的边都已被访问，边(u,v)就变成了连接v的后续分量的桥（没办法回来了），直接将v出栈输出，此时还要查看顶点u是否有别的未访问的边，只有当u其余未访问的边都被输出之后（必然会再次回到u，因为v后续分量必然含有奇度节点，初始节点也是奇度节点，如果不回到u，说明u后还有其他奇度节点，矛盾），才能输出(u,v)边，这样最后输出的顶点逆序就是一个欧拉路径（欧拉回路的证明更简单，略）。

算法实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def fleury(graph):
    start = None
    num = 0
    for k in graph:
        if len(graph(k))&1:
            num += 1
            start = k
    if num not in [0,2]:
        return False
    
    def dfs(v):
        S.append(v)
        while graph[v]:
            # 如果有边，过河拆桥，继续扩展
            u = graph[v].pop()
            graph[u].remove(v)
            dfs(u)
            break
            
    S = [start]
    res = []
    while S:
        top = S.pop()
        if graph[top]:
            # 如果栈顶有边，则继续扩展下去
            dfs(top)
        else:
            # 如果栈顶无边，说明栈顶与次栈顶之间的边是桥
            res.append(top)
    return res[::-1]
  • 算法分析：由于算法要经过每条边，所以时间必然是Ω(E)。在最坏情况下，在每个节点处进行一次 DFS，节点会重复走所以以边计算，算法复杂度应该是 O(E(E+V))

Hierholzer算法

  • 算法思想（以半欧拉图为例）：以一个奇度节点出发进行深度遍历，遍历的同时将经过的边删除（过河拆桥），如果某个节点不能继续遍历，则输出该节点。当遍历到u节点时，从该节点出发的深度遍历有两种结果：

    • 1）要么重新返回该节点（子环），如果该节点还有其他未访问的边，继续沿着该边深度遍历，仍有两种遍历结果，如果该顶点没有其他未访问的边，则可将环中的顶点输出
    • 2）要么在某个节点w处无法继续遍历，此时其所有邻接边都已访问，假设到达w的边为(v,w),此时(v-w)必然是w后分量的桥，因为u到w遍历过程必然包含了奇度节点，所以其他的遍历过程必然回到出发点，这就允许我们先从v开始得到在其他环中的欧拉路径后，再回到v，输出(v,w)边，输出w，最终得到的序列逆序即为一条欧拉路径。

  • 算法实现：有边过河拆桥，无边输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def hierholzer(graph):
    start = 0
    num = 0
    for k in graph:
        if len(graph(k))&1:
            num += 1
            start = k
    if num not in [0,2]:
        return False
        
    route = []
    # Hierholzer算法的核心只有三行代码：有边就过河拆桥，无边就输出
    def dfs(u):
        while graph[u]:
            dfs(graph[u].pop())
        route.append(u)
    
    dfs(start)
    return route[::-1]
  • 算法分析：时间复杂度是 O(E)，其在 DFS 的过程中不用恢复边，靠出栈记录轨。代码简洁，效率又高！！
坚持原创技术分享，您的支持将鼓励我继续创作！