数据结构与算法：数论

数论的理论部分详见 math 专题，本部分仅讨论数论相关的核心算法，及其在实际问题中的应用。

整除性与素数

辗转相除法

• 欧几里得算法（Euclidean algorithm）：也称为辗转相除法，通常用于计算两个整数的最大公约数，对$0\leqslant m<n$，EA用到以下递推式：

$$\begin{align*} &gcd(0,n)=n;\\ &gcd(m,n)=gcd(n\%m,m),\ m>0 \end{align*}$$

• 分析：时间复杂度为$O(lgn)$，具体证明参见拉梅定理

计算最大公约数

def gcd(m,n):
    """返回m,n的最大公约数。无所谓大小，m为除数，n为被除数"""
    while m:
        m,n = n%m,m
    return n

def gcd(m,n):
    """更加简洁的递归式"""
    return gcd(n%m,m) if m else n

计算最小公倍数

最小公倍数和最大公约数有以下关系：

$$gcd(m,n)*lcm(m,n)=m*n$$

def lcm(m,n):
    """返回m,n的最小公倍数"""
    return m * n /gcd(m,n)

求解贝祖方程

扩展欧几里得算法（Extended Euclidean algorithm）：在求得gcd(m,n)的同时，一定能找到整数x,y（其中一个可能是负数），使得它们满足贝祖等式：

$$mx + ny = gcd(m,n)$$

由欧几里得算法递推过程可得：

$$\left\{\begin{matrix} \begin{align*} &gcd(0,n)=n\\ &gcd(m,n)=gcd(n\%m,m)\\ &mx+ny=gcd(m,n)\\ &(n\%m)x_1+my_1=gcd(n\%m,m)\\ &n\%m=n-\left \lfloor \frac{n}{m} \right \rfloor m \end{align*} \end{matrix}\right.$$

整理化简得 a,b 的递推式 $xm+yn=(y_1-x_1\left \lfloor \frac{n}{m} \right \rfloor)m+x_1n$，即：

$$\left\{\begin{matrix} \begin{align*} &x=y_1-x_1\left \lfloor \frac{n}{m} \right \rfloor\\ &y=x_1\\ &x_{end}=0\\ &y_{end}=1 \end{align*} \end{matrix}\right.$$

def bz(m,n):
    """求解贝祖方程x*m+y*n=gcd(m,n)，返回一组(x,y)"""
    if m == 0:
        return 0,1
    x,y = bz(n%m,m)
    return y-x*(n/m),x

贝祖定理(Bézout’s identity)：整数不定方程 $mx+ny=c$ 有解（无穷多个解）的充要条件是$gcd(m,n)\mid c$。

如果贝祖方程有解，则一定有无穷解，设$(x_0,y_0)$是$mx+ny=gcd(m,n)$由辗转相除法得到的一个解，$d=gcd(m,n)$，则$mx+ny=c$的通解可表示为：

$$\left\{\left({\frac {c}{d}}x_{0}+{\frac {kn}{d}},\ {\frac {c}{d}}y_{0}-{\frac {km}{d}}\right)\mid k\in \mathbb {Z} \right\}$$

推论：$mx+ny=1$有解的充要条件为gcd(m,n)=1，即m,n互素。

[592] 分数加减运算

• 问题：给定一个表示分数加减运算表达式的字符串，你需要返回一个字符串形式的计算结果。 这个结果应该是不可约分的分数，即最简分数。 如果最终结果是一个整数，例如 2，你需要将它转换成分数形式，其分母为 1。所以在上述例子中, 2 应该被转换为 2/1。

输入:"-1/2+1/2"
输出: "0/1"

• 思路：通过最小公倍数通分，通过最大公约数约分
  1. 找到所有单元+-x/y，进而得到所有分子分母，
  2. 求分母最小公倍数
  3. 通分x*lcm/y求和，得到最终的分子、分母
  4. 最后再求最终分子分母的最大公约数
  5. 分子分母除以最大公约得到最简分数
• 代码：

def fractionAddition(self, expression):
    """
    :type expression: str
    :rtype: str
    """
    def gcd(a,b):
        if a < b:
            a,b = b,a
        while b:
            a,b = b,a%b
        return a
    def lcm(a,b):
        return a * b /gcd(a,b)
    
    parts = []
    part = ''
    for c in expression:
        if c in '+-':
            if part:
                parts.append(part)
                part = ''
        part += c
    if part: parts.append(part)
        
    x = []
    y = []
    for p in parts:
        cur = p.split('/')
        x.append(int(cur[0]))
        y.append(int(cur[1]))
    # print x,y,parts
    lcm_y = reduce(lcm,y)
    total_x = sum(x[i]*lcm_y/y[i] for i in range(len(x)))
    gcd_xy = abs(gcd(lcm_y,total_x))
    
    return '%d/%d'%(total_x/gcd_xy,lcm_y/gcd_xy)

[365] 水壶问题

• 问题：有两个容量分别为 x升 和 y升 的水壶以及无限多的水。请判断能否通过使用这两个水壶，从而可以得到恰好 z升 的水？如果可以，最后请用以上水壶中的一或两个来盛放取得的 z升 水。
• 思路：等价于ax+by=z有整数解(a,b)，且z <= x+y
• 代码：

def canMeasureWater(self, x, y, z):
    def gcd(m,n):
        while m:
            m,n = n%m,m
        return n
    g  = gcd(x,y)    
    return z % g == 0 and z <= x + y if g else not z

寻找 n 以内的素数

一般有”试除法“和”筛法“两种思路来寻找n以内的素数，这里介绍三种常用的方法：

方法	思路	空间	时间
优化试除法	对[2,n]中的每一个数k，试除[2,sqrt(k)]中所有素数，如果能整除说明k不是素数	O(1)	O(nlgn)
埃拉托斯特尼筛法	假设所有数都是素数，然后[2,sqrt(n)]间的素数p，将[p*p::p]的整数标记为非素数	O(n)	O(nlglgn)
线性筛法	每个合数都能唯一分解为最小素因子和一个小于自己的数之积，只用合数的最小素因子筛将其筛去，避免重复的筛选	O(n)	O(n)

[204] 计算质数

# 1. 试除法：4684 ms
def countPrimes(self, n):
        if n < 3:
            return 0
        res = [2]
        for k in xrange(3,n):
            i = 0
            tmp = int(k**0.5)
            while res[i] <= tmp:
                if k % res[i]:
                    i += 1
                else:
                    break
            else:
                res.append(k)
        return len(res)

# 2. 埃氏筛法：176ms，接近线性时间复杂度，实际效果竟然比线性筛还好
def countPrimes(self, n):
    if n < 3:
        return 0
    filt = [1] * n
    filt[0] = filt[1] = 0
    for i in xrange(2,int(n**0.5)+1):
        if filt[i]:
            filt[i*i::i] = [0] * ((n-1-i*i)/i + 1)
    return sum(filt)

# 3. 线性筛: 924ms 
def countPrimes(self, n):
    if n < 3:
        return 0
    prime = []
    filt = [1] * n
    filt[0] = filt[1] = 0
    for i in xrange(2,n):
        if filt[i]:
            prime.append(i)
        for p in prime:
            if i * p > n - 1:
                break
            filt[i*p] = 0
            # 如果i能被p整除，则i*后续素数的合数只能被p筛去
            if i % p == 0:
                break
    return sum(filt)      

扩展：以上思路很容易用来求解一个整数是否为素数、整数因式分解等问题。

算术基本定理

每一个正整数都能唯一地表示为素数幂积的形式，p代表所有可能的素数：

$$n=\prod_{p}p^{n_p},\ n_p\geqslant 0$$

[313] 超级丑数

• 问题：编写一段程序来查找第 n 个超级丑数。超级丑数是指其所有质因数都是长度为 k 的质数列表 primes 中的正整数。

输入: n = 12, primes = [2,7,13,19]
输出: 32 
解释: 给定长度为 4 的质数列表 primes = [2,7,13,19]，前 12 个超级丑数序列为：[1,2,4,7,8,13,14,16,19,26,28,32] 。

• 思路：

后续丑数必然是由已有丑数与质数列表中的质数乘积的结果，为了实现有序输出，可进行k路归并，丑数排序可以看做是k个有序表的归并排序
2*1，2*2，2*4，2*7...
7*1，7*2，7*4，7*7...
...
可以用k个指针指示每个有序表当前元素的下标，将较小的值放入总表，同时如果有序表中的值等于总表的值，下标要加1

• 代码：

def nthSuperUglyNumber(self, n, primes):
    """
    :type n: int
    :type primes: List[int]
    :rtype: int
    """
    k = len(primes)
    index = [0] * k
    ugly = [1]
    count = 1
    while count < n:
        cur = min(ugly[index[i]] * primes[i] for i in xrange(k))
        ugly.append(cur)
        count += 1
        for i in xrange(k):
            if ugly[index[i]] * primes[i] == cur:
                index[i] += 1
    return ugly[-1]

• 分析：时间复杂度O(kn)

模运算

定义模运算：n模m表示n除以m所得余数，记做$n\ mod\ m$或$n\%m$

$$n\ mod\ m = n - \left \lfloor \frac{n}{m} \right \rfloor m$$

• 模：mod后面的数称为模，至今还没有人给mod前面的数取名
• 余数：取模的结果，余数总是处于0和模之间
• 模运算可以推广到任意实数

模运算性质

mod运算的性质：以下性质都可以通过取模运算的定义来证明

• 四则运算法则：
  • $(a+b)\%c=(a\%c+b\%c)\%c$
  • $(a-b)\%c=(a\%c-b\%c)\%c$
  • $(ab)\%c=(a\%cb)\%c=(a\%c*b\%c)\%c$
  • $(a^b)\%c=((a\%c)^b)\%c$
  • $\frac{a}{b}\%c = a\bar{b}\%c,\ if\ b \mid a, b\perp c$
• 分配律：$c(a\%b)=(ca)\%(cb)$，是mod运算最重要的代数性质
• 模模律：$a\%c\%c=a\%c$

[523] 连续子数组和为k的倍数

• 问题：给定一个包含非负数的数组和一个目标整数 k，编写一个函数来判断该数组是否含有连续的子数组，其大小至少为 2，总和为 k 的倍数，即总和为 n*k，其中 n 也是一个整数。

输入: [23,2,6,4,7], k = 6
输出: True
解释: [23,2,6,4,7]是大小为 5 的子数组，并且和为 42。

• 思路：(a-b)%m=a%m-b%m，连续数组的和是k的倍数在k!=0时等价于能被k整除，等价于余数为0，等价于前i项和前j项和对k的模相等。记录模m第一次出现的位置，下次出现与首次出现隔了1个元素以上则返回True，初始没有元素设模为0，下标为-1.
• 代码:

def checkSubarraySum(self, nums, k):
    """
    :type nums: List[int]
    :type k: int
    :rtype: bool
    """
    d = {0:-1}
    total = 0
    for i,num in enumerate(nums):
        total += num
        tmp = total % (k or total+1)
        if tmp in d:
            if i > d[tmp] + 1:
                return True
        else:
            d[tmp] = i
    return False

大数取模

一般大数取模

对于某个大数，我们可以用字符串$s=a_1a_2…a_n$来存储，设f(n)代表前n个字符所组成的数值，则有:

$$\left\{\begin{matrix} \begin{align*} &f(n)=10f(n-1)+a_n\\ &f(1)=a_1 \end{align*} \end{matrix}\right.$$

利用取模四则运算法则来模拟手算竖式的方法:

$$\left\{\begin{matrix} \begin{align*} &f(n)\% m=(f(n-1)\% m \times 10+a_n)\%m\\ &f(1)\%m=a_1 \%m \end{align*} \end{matrix}\right.$$

代码:

def get_mod(s,m):
    res = 0
    for c in s:
        res = (res%m * 10 + int(c))%m
    return res

快速幂模

• 蒙哥马利(Montgomery)幂模运算是快速计算a^b%k的一种算法，是RSA加密算法的核心之一。设$f(c,e,n)=c^e\%n$，则有以下递推式：

$$\left\{\begin{matrix} \begin{align*} &f(c,e,n)=f(c,e-1,n)*c\%n=f(c^2\%n,e>>1,n)*c\%n,\ if\ e\&1=1\\ &f(c,e,n)=f(c^2\%n,e>>1,n),\ else \end{align*} \end{matrix}\right.$$

代码：

# 时间复杂度为lge
def quick_mod(base,exp,mod):
    res = 1
    while exp:
        if exp & 1:
            res = res * base % mod
        base, exp = base * base % mod, exp >> 1  
    return res
    
# 递归更简洁
def quick_mod(base,exp,mod):
    if exp == 0:
        return 1%mod
    return (Montgomery1(base*base%mod,exp>>1,mod)*[1,base%mod][exp&1])%mod

[372] 超级次方——幂模

• 问题：你的任务是计算 a^b 对 1337 取模，a 是一个正整数，b 是一个非常大的正整数且会以数组形式给出。
• 思路：快速取模,取模的乘法法则(ab)%m=(a%mb%m)%m，f(a,b0+b110+…) = (a^b0%m f(a^10,b1+b2*10+…))%m
• 代码:

def superPow(self, a, b):
    """
    :type a: int
    :type b: List[int]
    :rtype: int
    """
    res = 1
    base = a
    for n in b[::-1]:
        res = (res * self.quick_mod(base,n,1337)) % 1337
        base = self.quick_mod(base,10,1337)
    return res

def quick_mod(self,base,exp,mod):
    res = 1
    while exp:
        if exp & 1:
            res = res * base % mod
        base = base * base % mod
        exp >>= 1
    return res

其他数论问题

勾股素数

• 问题：找到<=n的素勾股数 和 不能构成勾股数的边的长度个数。如果 (a, b, c) 是勾股数，它们的正整数倍数，也是勾股数，即 (na, nb, nc) 也是勾股数。若果 a, b, c 三者互质（它们的最大公因数是 1），它们就称为素勾股数。
• 思路：

以下的方法可用来找出勾股数。设 m > n 、 m 和 n 均是正整数，

a = m2 − n2,
b = 2mn,
c = m2 + n2
若 m 和 n 是互质，而且 m 和 n 其中有一个是偶数，计算出来的 a, b, c 就是素勾股数。（若 m 和 n 都是奇数， a, b, c 就会全是偶数，不符合互质。）

所有素勾股数可用上述列式当中找出，这亦可推论到数学上存在无穷多的素勾股数。

• 代码:

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>

using namespace std;

bool vis[1000010];

int gcd(int x,int y)
{
    return y==0?x:gcd(y,x%y);
}

int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        int cnt = 0,num = 0;
        memset(vis,0,sizeof(vis));
        for(int i=1;i<=sqrt(n);i++)
        {
            for(int j=i+1;j<=sqrt(n);j++)
            {
                int x = j*j-i*i;
                int y = 2*i*j;
                int z = i*i+j*j;

                if(x<=n && y<=n && z<=n)
                {
                    if(!vis[x]) vis[x] = true,cnt++;
                    if(!vis[y]) vis[y] = true,cnt++;
                    if(!vis[z]) vis[z] = true,cnt++;
                    int f = n/z;
                    for(int k=1;k<=f;k++)
                    {
                        int nx = x*k,ny = y*k,nz = z*k;
                        if(!vis[nx]) vis[nx] = true,cnt++;
                        if(!vis[ny]) vis[ny] = true,cnt++;
                        if(!vis[nz]) vis[nz] = true,cnt++;
                    }
                    if(gcd(i,j)==1)
                    {
                        if(((i&1) && (j&1)==0) || ((j&1) && (i&1)==0))
                        num++;
                    }
                }
            }
        }
        printf("%d %d\n",num,n-cnt);
    }
    return 0;
}

整数-序列转化

这可能是最常用的操作了

def n2s(n):
    """将整数n转化为字符串"""
    if n == 0:
        return '0'
    res = ''
    while n:
        div,mod = divmod(n,10)
        n = n/10
        res = str(mod) + res
    return res
    
def s2n(s):
    """将字符串转化为整数"""
    res = 0
    for c in s:
        res = res * 10 + int(c)
    return res 

[171] Excel列名转列号

• 问题:给定一个Excel表格中的列名称，返回其相应的列序号

A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28 
...

• 思路：26进制转化为10进制
• 代码：

def titleToNumber(self, s):
    c2i = lambda x:ord(x)-ord('A')+1
    res = 0
    for i,c in enumerate(s):
        res = res * 26 + c2i(c) 
    return res

[168] Excel列号转列名

• 问题：给定一个正整数，返回它在 Excel 表中相对应的列名称
• 思路：难点在于A表示1而不是0，Ai26**i = ai26^i+26^i，a026^0+26^0 + a126^1+26^1 + … + =n，(n-1)/26 = a1*26^0 + 26^0+…转化为子问题，因此n = (n-1)/26，a0 = (n-1)%26 0~25对应A~Z
• 代码：

def convertToTitle(self, n):
    ans = ''
    while n:
        ans = chr(ord('A') + (n - 1) % 26) + ans
        n = (n - 1) / 26
    return ans

[812] 三点构成最大面积

• 问题:给定包含多个点的集合，从其中取三个点组成三角形，返回能组成的最大三角形的面积
• 思路：遍历所有可能的三点组合，求出最大面积，核心在于已知三点如何求三点构成的三角形的面积，设A(x1,y1),B(x2,y2),C(x3,y3)，则三角形面积可以表示为AB与AC叉乘绝对值的一半：

          i      j
        x2-x1, y2-y1
AB×AC =              = (x2-x1)*(y3-y1)-(x3-x1)*(y2-y1)
        x3-x1, y3-y1
S(ABC) = 0.5*abs(AB×AC)

• 代码：

def largestTriangleArea(self, points):
    """
    :type points: List[List[int]]
    :rtype: float
    """
    def area(a,b,c):
        x1,y1,x2,y2,x3,y3 = a[0],a[1],b[0],b[1],c[0],c[1]
        return 0.5 * abs((x2-x1)*(y3-y1)-(x3-x1)*(y2-y1))
    
    n = len(points)
    res = 0
    for i in xrange(n-2):
        for j in xrange(i+1,n-1):
            for k in xrange(j+1,n):
                res = max(res, area(points[i], points[j], points[k]))
    
    return res

[593] 四点是否构成正方形

• 问题：给定二维空间中四点的坐标，返回四点是否可以构造一个正方形
• 思路:正方形充要条件：四条边相等，对角线相等>0;识别对角点的方法：如果是正方形，则排序后，第一个点代表左下点，最后一个点代表右上点，它们必是对角顶点
• 代码:

def validSquare(self, p1, p2, p3, p4):
    """
    :type p1: List[int]
    :type p2: List[int]
    :type p3: List[int]
    :type p4: List[int]
    :rtype: bool
    """
    dis = lambda x,y:(x[0]-y[0])**2 + (x[1]-y[1])**2
    p = [p1,p2,p3,p4]
    p.sort()
    if dis(p[0],p[1]) == dis(p[0],p[2]) == dis(p[3],p[1]) == dis(p[3],p[2]) > 0:
        if dis(p[0],p[3]) == dis(p[1],p[2]):
            return True
    return False

[223] 矩形面积

• 问题:在二维平面上计算出两个由直线构成的矩形重叠后形成的总面积。每个矩形由其左下顶点和右上顶点坐标表示，如图所示。

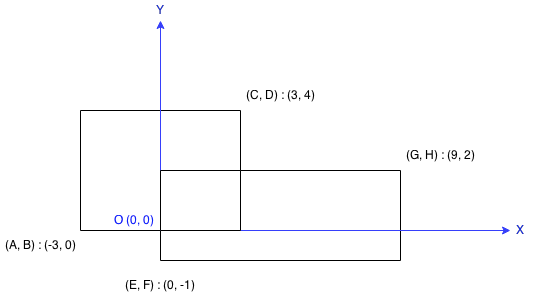
• 思路:转化为求交集的面积sum() = max(0,min(D,H)-max(B,F)) * max(0,min(C,G)-max(A,E))
• 代码:

def computeArea(self, A, B, C, D, E, F, G, H):
        """
        :type A: int
        :type B: int
        :type C: int
        :type D: int
        :type E: int
        :type F: int
        :type G: int
        :type H: int
        :rtype: int
        """
        total = (D-B) * (C-A) + (G-E) * (H-F)
        return total - max(0,min(D,H)-max(B,F)) * max(0,min(C,G)-max(A,E))

[453] 最小移动次数使数组元素相等

• 问题:给定一个长度为 n 的非空整数数组，找到让数组所有元素相等的最小移动次数。每次移动可以使 n - 1 个元素增加 1

输入:
[1,2,3]

输出:
3

解释:
只需要3次移动（注意每次移动会增加两个元素的值）：

[1,2,3]  =>  [2,3,3]  =>  [3,4,3]  =>  [4,4,4]

• 思路：：一次移动将n - 1个元素加1，等价于将剩下的1个元素减1。因此累加数组中各元素与最小值之差即可
• 代码:

def minMoves(self, nums):
    """
    :type nums: List[int]
    :rtype: int
    """
    return sum(nums) - min(nums) * len(nums)

[462] 最少移动次数使数组元素相等 II

• 问题：给定一个非空整数数组，找到使所有数组元素相等所需的最小移动数，其中每次移动可将选定的一个元素加1或减1

输入:
[1,2,3]
输出:
2
说明：
只有两个动作是必要的（记得每一步仅可使其中一个元素加1或减1）： 
[1,2,3]  =>  [2,2,3]  =>  [2,2,2]

• 思路：中位数定理：当a取x中的中位数时，绝对残差和sum(|x-a|)最小
• 代码:

import random
class Solution(object):
    def minMoves2(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        n = len(nums)
        median = self.findKthLargest(nums,0,n-1,(n-1)/2+1)
        return sum(abs(num-median) for num in nums)
        
    def findKthLargest(self, nums, l, r, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: int
        """
        
        pivot = self.partition(nums,l,r)
        if pivot == k - 1:
            return nums[pivot]
        elif pivot < k - 1:
            return self.findKthLargest(nums, pivot+1, r, k)
        else:
            return self.findKthLargest(nums, l, pivot-1, k)
        
    
    def partition(self,nums,low,high):
        rand = random.randint(low,high)
        nums[rand],nums[low] = nums[low],nums[rand]
        
        bag = low
        for i in range(low+1,high+1):
            if nums[i] <= nums[low]:
                bag += 1
                nums[bag],nums[i] = nums[i], nums[bag]
        nums[bag], nums[low] = nums[low],nums[bag]
        return bag

[517] 超级洗衣机——均衡

• 问题:假设有 n 台超级洗衣机放在同一排上。开始的时候，每台洗衣机内可能有一定量的衣服，也可能是空的。在每一步操作中，你可以选择任意 m （1 ≤ m ≤ n） 台洗衣机，与此同时将每台洗衣机的一件衣服送到相邻的一台洗衣机。给定一个非负整数数组代表从左至右每台洗衣机中的衣物数量，请给出能让所有洗衣机中剩下的衣物的数量相等的最少的操作步数。如果不能使每台洗衣机中衣物的数量相等，则返回 -1。
• 思路:

讨论每个元素处的情形，记l,r代表i元素左右两侧和超出平均水平的值，讨论三种情形：
        1. l >=0,r>=0，两边一定会流向i，可同时进行，需要次数max(l,r)
        2. l < 0,r < 0,i一定会流向两边，不可同时进行，需要次数-l-r
        3. 其他情形流经i的元素需要有max(abs(l),abs(r))次流动

• 代码：

def findMinMoves(self, machines):
    """
    :type machines: List[int]
    :rtype: int
    """
    n = len(machines)
    total = sum(machines)
    if total % n:
        return -1
    avg = total/n
    l,r = 0,0
    res = 0
    for i, num in enumerate(machines):
        r += avg - num
        if l >= 0 and r >= 0:
            res = max(res,max(l,r))
        elif l < 0 and r < 0:
            res = max(res,abs(l)+abs(r))
        else:
            res = max(res,abs(l),abs(r))
        l += num - avg
    return res

[319] 灯泡开关

• 问题：初始时有 n 个灯泡关闭。 第 1 轮，你打开所有的灯泡。 第 2 轮，每两个灯泡你关闭一次。 第 3 轮，每三个灯泡切换一次开关（如果关闭则开启，如果开启则关闭）。第 i 轮，每 i 个灯泡切换一次开关。 对于第 n 轮，你只切换最后一个灯泡的开关。 找出 n 轮后有多少个亮着的灯泡。
• 思路：对于第i个灯泡，当i的因子个数为奇数时，最终会保持点亮状态，例如9的因子为1，3，9，当且仅当i为完全平方数时，其因子个数为奇数，另外1~n中完全平方数的个数为n**0.5
• 代码:

def bulbSwitch(self, n):
    return int(n**0.5)

[172] 阶乘后的零

• 问题：给定一个整数 n，返回 n! 结果尾数中零的数量
• 思路：n!后缀0的个数 = n!质因子中5的个数 = floor(n/5) + floor(n/25) + floor(n/125) + ….
• 代码：

def trailingZeroes(self, n):
    res = 0
    while n:
        res += n/5
        n = n/5
    return res

[343] 整数拆分

• 问题:给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。例如，给定 n = 2，返回1（2 = 1 + 1）；给定 n = 10，返回36（10 = 3 + 3 + 4）。注意：你可以假设 n 不小于2且不大于58。
• 思路：向下分解到3就不能再分了
  • 如果刚好，返回3**(n/2)
  • 如果余1，就把1加到3上构成4
  • 如果余2，乘2
• 代码：

def integerBreak(self, n):
    mod = n % 3
    if mod == 0:
        return 3 ** (n/3) if n > 3 else 2
    elif mod == 1:
        return 3 ** (n/3-1) * 4
    else:
        return 3 ** (n/3) * 2 if n > 2 else 1

[279] 完全平方数——四平方和定理

• 问题：给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

• 思路1：动态规划，状态转移方程dp[n] = min(dp[n-i^2]) + 1,if n不是完全平方数，如果是完全平方数返回1，时间复杂度O(n * sqrt n)；
• 思路2：四平方和定理：任何自然数都可以用最多四个平方和数之和，且只有当$n=4^a(8b+7)$时才需要最少四个平方数之和；
• 代码：

# 思路1
def numSquares(self, n):
    if int(n**0.5)**2 == n:
        return 1
    res = 1
    lst = [i*i for i in xrange(1,int(n**0.5)+1)]
    Q = set(lst)
    while n not in Q:
        res += 1
        Q = set(q+x for q in Q for x in lst if q+x<=n)
        
    return res

# 思路2:
def numSquares(self, n):
    while n & 3 == 0:
        n >>= 2
    if n & 7 == 7:
        return 4
    for a in xrange(int(n**0.5)+1):
        b = int((n - a * a)**0.5)
        if a * a + b * b == n:
            return (a != 0) + (b!=0)
    return 3

[368] 最大整除子集

• 问题：给出一个由无重复的正整数组成的集合, 找出其中最大的整除子集, 子集中任意一对 (Si, Sj) 都要满足: Si % Sj = 0 或 Sj % Si = 0。如果有多个目标子集，返回其中任何一个均可

集合: [1,2,3]
结果: [1,2] (当然, [1,3] 也正确)

• 思路：动态规划，dp[x] = max(dp[x], dp[y] + 1) 其中： 0 <= y < x 且 nums[x] % nums[y] == 0记录最大路径，只需每次转移时，记录x的父节点，最后即可从最大DP处追溯到整条最大的路径
• 代码：

def largestDivisibleSubset(self, nums):
    """
    :type nums: List[int]
    :rtype: List[int]
    """
    if not nums:
        return []
    nums.sort()
    n = len(nums)
    dp =[1] * n
    pre = [None] * n
    for i in xrange(1,n):
        for j in xrange(i):
            if nums[i] % nums[j] == 0 and dp[j] + 1 > dp[i]:
                dp[i] = dp[j] + 1
                pre[i] = j
    start = dp.index(max(dp))
    
    res = []
    while start is not None:
        res.append(nums[start])
        start = pre[start]
    return res[::-1]

[670] 最大交换

• 问题：给定一个非负整数，你至多可以交换一次数字中的任意两位。返回你能得到的最大值。

输入: 2736
输出: 7236
解释: 交换数字2和数字7。

• 思路：从后向前，记录当前后缀中最大元素的位置，相等算后面的；从前向后，如果当前位置元素小于后续最大元素，则交换二者；
• 代码:

def maximumSwap(self, num):
    """
    :type num: int
    :rtype: int
    """
    num = map(int,str(num))
    n = len(num)
    
    max_id = range(n)
    for i in xrange(n-2,-1,-1):
        if num[i] <= num[max_id[i+1]]:
            max_id[i] = max_id[i+1]
    
    for j in xrange(n):
        if num[j] < num[max_id[j]]:
            num[j],num[max_id[j]] = num[max_id[j]],num[j]
            break
    
    return int(''.join(map(str,num)))

[754] 到达终点数字

• 问题:在一根无限长的数轴上，你站在0的位置。终点在target的位置。每次你可以选择向左或向右移动。第 n 次移动（从 1 开始），可以走 n 步。返回到达终点需要的最小移动次数。

输入: target = 2
输出: 3
解释:
第一次移动，从 0 到 1 。
第二次移动，从 1 到 -1 。
第三次移动，从 -1 到 2 。

• 思路:

分情况讨论：
    1. 1+2+。。。+k=target，则返回k
    2. 1+2+...+k刚好大于target，如果多出d为偶数，则只需将d/2反向即可，返回k
    3. 如果d为奇数，任何数的反向都只会改变偶数次，k次达不到，这时+k+1差距如果是偶数，返回k+1，
    4. 如果是奇数,返回k+2，因为必能在k次达到target-1，再经过两次+k-(k+1)

• 代码：

import math
def reachNumber(self, target):
    n = abs(target)
    # 解二次方程
    k = int(math.ceil(((8*n+1)**0.5-1)/2.))
    total = k*(k+1)/2
    d = total - n
    if d % 2 == 0:
        return k
    elif (d+k+1) % 2 == 0:
        return k + 1
    else:
        return k + 2

• 分析：时间复杂度O(1)

[50] 快速幂

• 问题：实现 pow(x, n) ，即计算 x 的 n 次幂函数
• 思路:

快速计算幂：时间复杂度lgn
    1. x^n = (x^2)^(n>>2),if n & 1 == 0
    2. x^n = (x^2)^(n>>2) * x,if n & 1 
    3. 边界如果是正数则n=0，负数则n=-1

• 代码:

def myPow(self, x, n):
    """
    :type x: float
    :type n: int
    :rtype: float
    """
    if n == 0:
        return 1.
    if n == -1:
        return 1./x
    return self.myPow(x*x, n>>1)*[1,x][n&1]

[829] 连续整数求和

• 问题:给定一个正整数 N，试求有多少组连续正整数满足所有数字之和为 N?

输入: 9
输出: 3
解释: 9 = 9 = 4 + 5 = 2 + 3 + 4

• 思路:

思路2：假设连续数组长度为c，那么和为N的数组满足：
    1. 如果c为奇数，N/c为整数
    2. 如果c为偶数，(N/c+0.5)*c=N
    同时，要求为正整数，如果c(c+1)/2>N，break

• 代码：

def consecutiveNumbersSum(self, N):
    """
    :type N: int
    :rtype: int
    """
    c = 1
    res = 0
    while c <= N:
        if c*(c+1)/2 > N:
            break
        if c & 1:
            res += N % c == 0
        else:
            res += N / c * c + c / 2 == N
        c += 1
    return res

[400] 第N个数字

• 问题：在无限的整数序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …中找到第 n 个数字。

输入:
11
输出:
0
说明:
第11个数字在序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... 里是0，它是10的一部分。

• 思路:

1   1-9
2   10-99
3   100-999
4   1000-9999
5   10000-99999
6   100000-999999
7   1000000-9999999
8   10000000-99999999
9   100000000-99999999
先确定所属段，再确定所属整数，再确定对应字符

• 代码:

def findNthDigit(self, n):
    for i in xrange(10):
        delta = 9 * 10 ** i
        if n <= delta * (i+1):
            break
        n -= delta * (i+1)
    
    number = str((n - 1) / (i + 1) + 10 ** i)
    index  = (n - 1) % (i + 1)
    return int(number[index])

[233] 数字1的个数

• 问题：给定一个整数 n，计算所有小于等于 n 的非负整数中数字 1 出现的个数。
• 思路:

分类讨论1在各个位上出现的次数：if n = xyzdabc，现讨论千位上的1出现的次数
    (1) xyz * 1000                     if d == 0  xy(z-1)1000~xy(z-1)1999:1000~1999
    (2) xyz * 1000 + abc + 1           if d == 1  xyz1000~xyz1abc
    (3) xyz * 1000 + 1000              if d > 1   xyz1000~xyz1999
对每一位上1出现的次数加和即可

• 代码:

def countDigitOne(self, n):
    if n < 1:
        return 0
    res = 0
    n = str(n)
    k = len(n)
    for i,c in enumerate(n):
        left  = int(n[:i] or 0)
        mid   = int(n[i])
        right = int(n[i+1:] or 0)
        cur = 10 ** (k-i-1)
        if mid == 0:
            res += left * cur
        elif mid == 1:
            res += left * cur + right + 1
        else:
            res += left * cur + cur
    return res

[43] 字符串相乘

• 问题: 给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

输入: num1 = "123", num2 = "456"
输出: "56088"

• 思路: 模拟手动乘法，从后向前，div,mod=divmod(xi*yj,10)，mod存放在数组res的i+j位，div存放在i+j+1位，最后从后向前遍历res，div,mod=divmod(res[i],10)，mod留到i位，div加到i+1位，结束时如果div不为0则创建新的位来存

• 代码:

def multiply(self, num1, num2):
    """
    :type num1: str
    :type num2: str
    :rtype: str
    """
    m,n = len(num1),len(num2)
    res =[0] * (m + n)
    num1,num2 = num1[::-1],num2[::-1]
    for i in xrange(m):
        for j in xrange(n):
            div,mod = divmod(int(num1[i])*int(num2[j]),10)
            res[i+j] += mod
            res[i+j+1] += div
    
    for k in xrange(m+n-1):
        div,mod = divmod(res[k], 10)
        res[k] = mod
        res[k+1] += div
    
    count = m + n
    while count > 1 and res[-1] == 0:
        res.pop()
        count -= 1
    
    return ''.join(map(str,res[::-1]))

不使用乘除的除法

• 问题：给定两个整数，被除数 dividend 和除数 divisor。将两数相除，要求不使用乘法、除法和 mod 运算符。

输入: dividend = 7, divisor = -3
输出: -2

• 思路：a/b=c，则：a = bc + m=(b2^k1 + b 2^k2 + …b2^0 + m)，尝试用被除数减y的231…20倍数，如果减得动则把相应的倍数加到商中，如果减不动则尝试更小的倍数
• 代码:

def divide(self, dividend, divisor):
    """
    :type dividend: int
    :type divisor: int
    :rtype: int
    """
    mark = (dividend >= 0) == (divisor >= 0)
    x, y = map(abs,[dividend, divisor])
    res = 0
    for i in xrange(31,-1,-1):
        if x >> i >= y:
            res += 1 << i
            x -= y << i
    return min(2**31-1,res) if mark else max(-2**31,-res)

[166] 分数到小数

• 问题：给定两个整数，分别表示分数的分子 numerator 和分母 denominator，以字符串形式返回小数。如果小数部分为循环小数，则将循环的部分括在括号内。

输入: numerator = 2, denominator = 3
输出: "0.(6)"

• 思路:

思路：模拟手除法
    1. 首先算出整数部分n/m和余数部分n%m，如果n和m有负号，将符号单独拿出
    2. 余数不为零，或者不在余数字典{余数:最后出现的位置}中，则将余数放在余数字典，同时余数*10再除被除数，记录值和新的余数
    3. 如果余数为0，则将当前的整数和小数部分组合
    4. 如果余数不为0，则将当前整数和小数部分组合，同时找到当前余数上次出现的位置，加上括号

• 代码:

def fractionToDecimal(self, numerator, denominator):
    """
    :type numerator: int
    :type denominator: int
    :rtype: str
    """
    flag = '-' * (numerator ^ denominator < 0 and numerator != 0)
        
    n,m = abs(numerator), abs(denominator)
    inter = n/m
    n = n% m
    
    mod = {}
    dec = []
    index = 0
    while n and n not in mod:
        mod[n] = index
        n *= 10
        dec.append(n/m)
        index += 1
        n %= m
    
    if n == 0:
        if dec:
            decimal = '.%s'%(''.join(map(str,dec)))
        else:
            decimal = ''
    else:
        decimal = '.%s(%s)'%(''.join(map(str,dec[:mod[n]])),''.join(map(str,dec[mod[n]:index])))
    
    return '%s%d%s'%(flag, inter, decimal)

[149] 直线上最多的点数——按起点分类

• 问题：给定一个二维平面，平面上有 n 个点，求最多有多少个点在同一条直线上。

输入: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出: 4
解释:
^
|
|  o
|     o        o
|        o
|  o        o
+------------------->
0  1  2  3  4  5  6

• 思路1：对于每个点统计其他点到它的斜率出现的次数，次数最大的斜率，对应共线点数最多的直线；需注意如果横坐标相同时记斜率为None；可能含有重复的点，重复的点可以算作任何斜率
• 思路2：RANSAC (Random sample consensus)算法，每次随机抽出一对点，找到所有和他们共线的点数，只需要重复几十次抽样就可以得到正确结果（但不保证每次都能成功）
• 代码：

# 思路1:
def maxPoints(self, points):
    """
    :type points: List[Point]
    :rtype: int
    """
    def slope(point1,point2):
        if point1.x == point2.x:
            return None
        else:
            return 100.*(point2.y - point1.y)/(point2.x-point1.x)
    
    n = len(points)
    res = 0 
    for i in xrange(n):
        d = collections.Counter()
        same = 1
        for j in xrange(i+1,n):
            
            if points[i].x == points[j].x and points[i].y == points[j].y:
                same += 1
            else:
                d[slope(points[i],points[j])] += 1
        if d:
            res = max(res, d.most_common(1)[0][1] + same)
        else:
            res = max(res, same)
            
    return res

# 思路2
def maxPoints(self, points):
    """
    :type points: List[Point]
    :rtype: int
    """
    def get_pairs():
        while True:
            index1, index2 = random.sample(xrange(n), 2)
            p1,p2 = points[index1],points[index2]
            if p1.x != p2.x or p1.y != p2.y:
                return p1, p2
    
    n = len(points)
    s = {(p.x, p.y) for p in points}
    if n < 2 or len(s) == 1:
        return n
    
    res = 0
    for i in xrange (0,50): 
        p1, p2 = get_pairs()
        cur = 0
        for j in xrange(n):
            p3 = points[j]
            if (p2.y-p1.y) * (p3.x-p1.x) == (p2.x-p1.x) * (p3.y-p1.y):
                cur += 1
        res = max(res, cur)
                
    return res   

[810] 黑板异或游戏（位运算）

• 问题：一个黑板上写着一个非负整数数组 nums[i] 。小红和小明轮流从黑板上擦掉一个数字，小红先手。如果擦除一个数字后，剩余的所有数字按位异或运算得出的结果等于 0 的话，当前玩家游戏失败。 (另外，如果只剩一个数字，按位异或运算得到它本身；如果无数字剩余，按位异或运算结果为 0。）换种说法就是，轮到某个玩家时，如果当前黑板上所有数字按位异或运算结果等于 0，这个玩家获胜。假设两个玩家每步都使用最优解，当且仅当小红获胜时返回 true。
• 思路：

  bit  :      3 2 1 0
---------------------
num1 : 10 | 1 0 1 0 
num2 : 11 | 1 0 1 1
num3 : 1  | 0 0 0 1
num4 : 2  | 0 0 1 0
num5 : 2  | 0 0 1 0
num6 : 8  | 1 0 0 0
--------------------
XOR  : 8  | 1 0 0 0
   如果开始时xor(nums) = 0，则A赢
   如果开始时xor(nums) !=0，如果len(nums)是偶数，则A赢，反之B赢。
      1. A只需要先找到xor(nums)中为1的二进制位，数组中必存在该位为0的元素（否则偶数个元素的异或就变成0了），A选择移去该元素，对该位的结果无影响，xor(nums) !=0
      2. B做选择，B随便做什么选择，A要么赢，要么回到上一轮同样的状态，偶数个元素异或不为0，选择不能无限持续下去，最终必然无论B选什么，异或结果都会变成0

• 代码:

def xorGame(self, nums):
    """
    :type nums: List[int]
    :rtype: bool
    """
    return reduce(lambda x,y:x^y, nums) == 0 or len(nums) & 1 == 0