数据结构与算法：排序算法

发表于 | 更新于: | 分类于 | 阅读次数:
字数统计: 3.5k | 阅读时长 ≈ 14

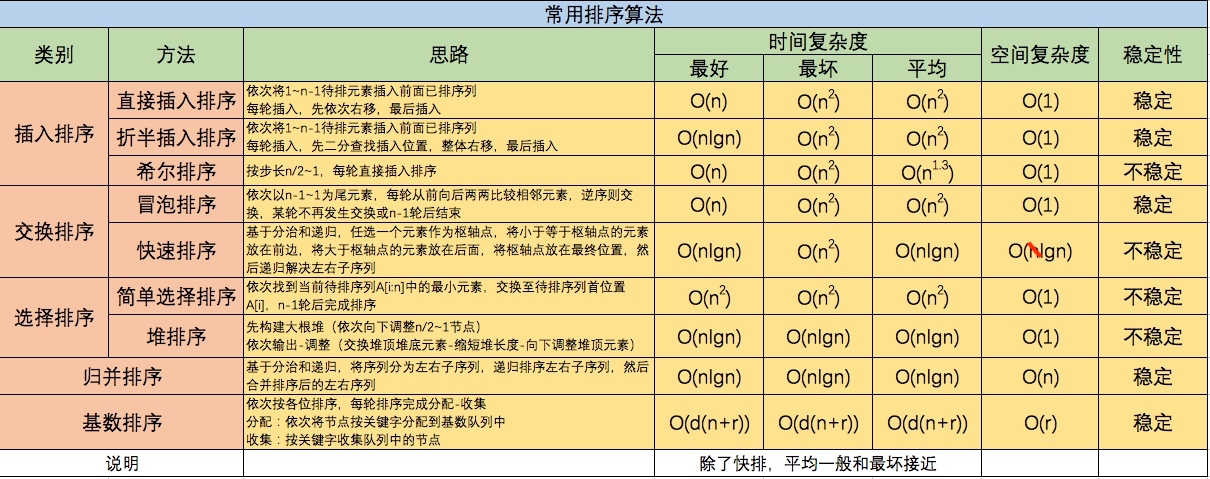
排序就是使列表元素按照关键字递增或递减排列的过程。排序算法的时间复杂度一般是由比较和移动的次数决定的。(待补充计数排序、桶排序代码、排序基本概念、外排序等)

插入排序(Insertion Sort)

基本思想：每次将一个待排元素插入到前面已排序列中，直至全部插入。

直接插入排序

  • 思路：从1到n-1依次将待排元素插入到前面已排序列中，每次插入时，从后向前遍历已排序列，如果大于待排元素则后移一位，如果不大于待排元素或达到首部则插入待排元素。
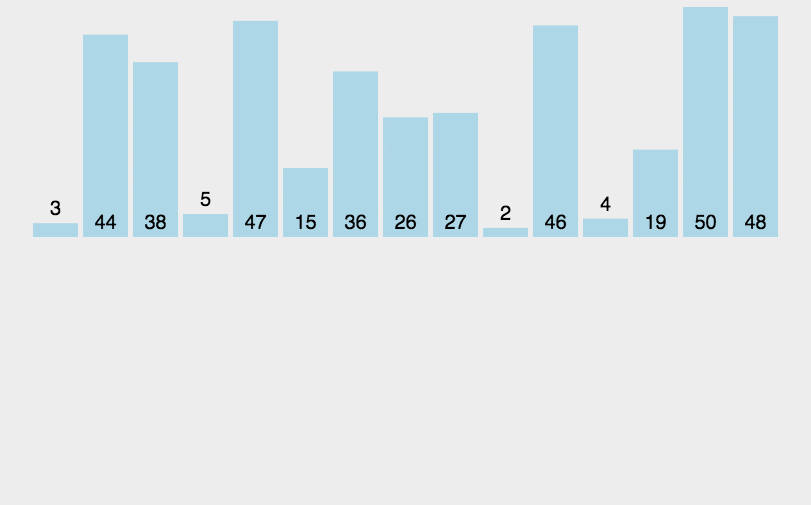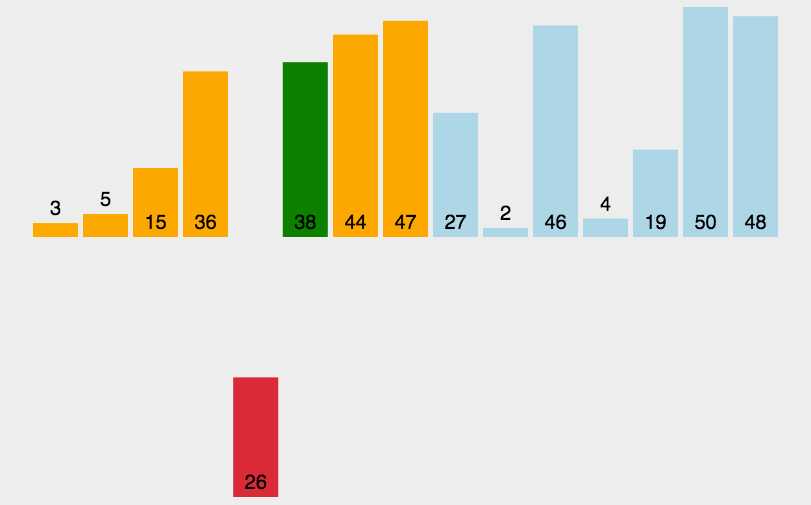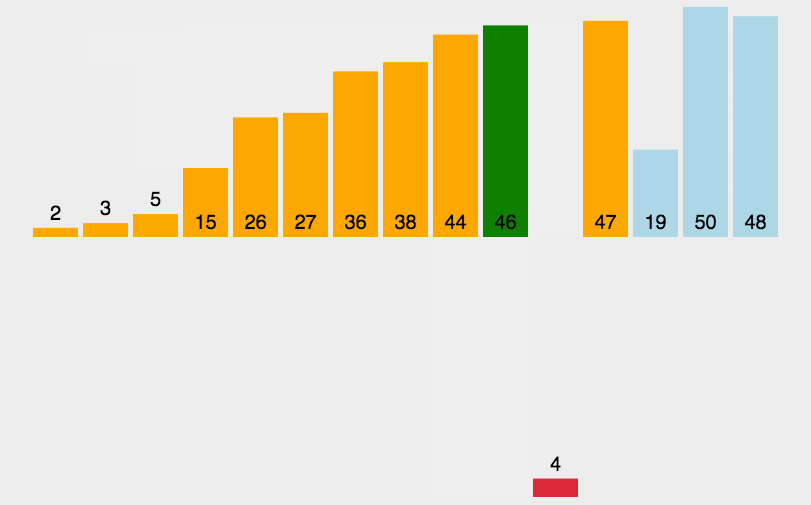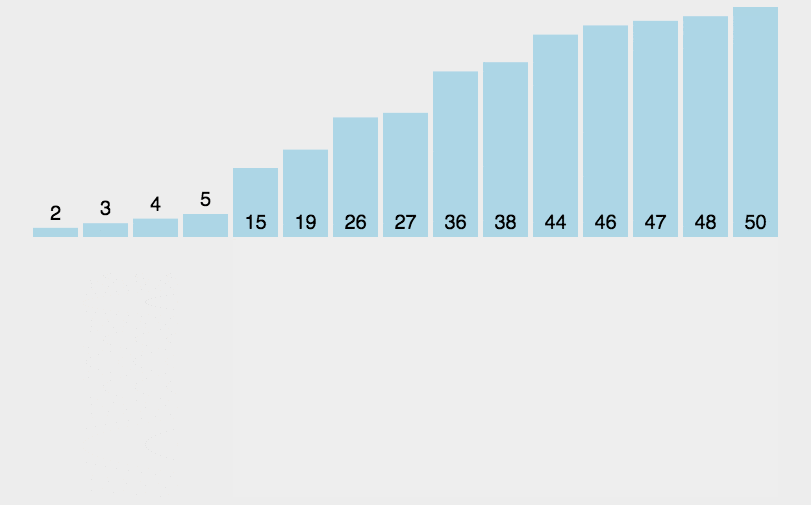
  • 实现：
1
2
3
4
5
6
7
def insert_sort(A):
    for i in xrange(1,len(A)):
        cur,j = A[i],i-1
        while j>=0 and A[j]>cur:
            A[j+1] = A[j]
            j -= 1
        A[j+1] = cur
  • 分析：
    • 时间复杂度：
      • 最好情况，元素已有序，仅需比较n次，无需移动，O(n);
      • 最坏情况，元素反序，O(n ^ 2)
    • 空间复杂度：O(1)
    • 稳定性：每次只会交换相邻元素，稳定
    • 适用：顺序表和链表

折半插入排序

  • 思路：折半插入是直接插入的一个变种，在每次插入新的待排元素时，先使用二分查找在前面有序序列中找到插入位置，再统一移动插入位置到旧位置间的元素，最后插入待排元素

  • 实现：

1
2
3
4
5
6
7
8
def binsert_sort(A):
    for i in xrange(1,len(A)):
        l,r = 0,i-1
        while l <= r:
            mid = (l+r)/2
            if A[i] < A[mid]: r = mid - 1
            else: l = mid + 1
        A[r+2:i+1],A[r+1] = A[r+1:i],A[i]
  • 分析：
    • 时间复杂度：只减少了比较次数O(lgn)但并没有改变移动次数，仍为O(n^2)
    • 空间复杂度：O(1)
    • 稳定性：不改变相等元素的原始相对位置，稳定
    • 适用：顺序表

希尔(插入)排序(shell sort)

直接插入排序在规模较小或序列基本有序时效率较高，希尔排序正是先将序列减小规模，基本有序来提高直接插入排序的效率。

  • 思想：按步长从n/2到1，反复进行直接插入排序。
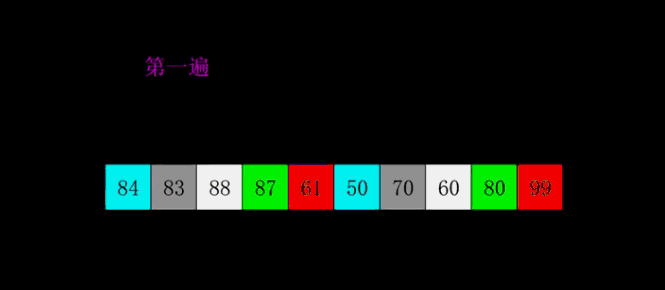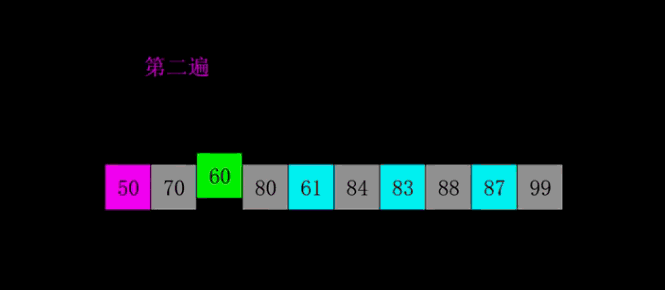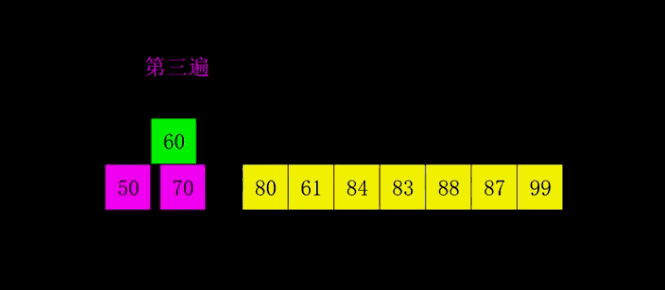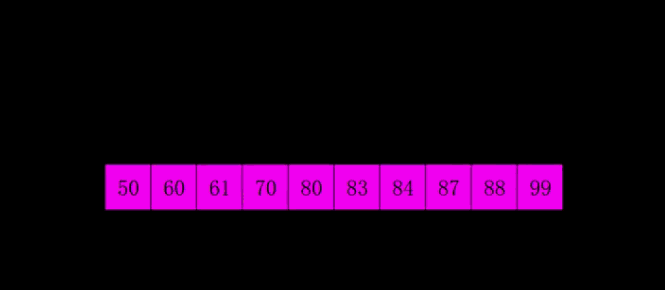
  • 实现：
1
2
3
4
5
6
7
8
9
10
11
def shell_sort(A):
    n = len(A)
    d = n/2
    while d:
        for i in xrange(d,n):
            cur,j = A[i],i-d
            while j>=0 and A[j]>cur:
                A[j+d] = A[j]
                j -= d
                A[j+d] = cur
        d = d/2
  • 分析：
    • 时间复杂度：平均O(n^1.3)，最坏O(n ^ 2)
    • 空间复杂度：O(1)
    • 稳定性：当两个相同的元素被分到不同子组时顺序可能改变，不稳定
    • 适用：顺序表

交换排序

思想：根据序列中两个元素的比较结果来交换它们的位置。

冒泡排序(bubble sort)

  • 思想：从前向后两两比较相邻元素，若逆序则交换；每轮冒泡都将当前最大元素排到最终位置（该元素不再参与下一轮排序），某轮冒泡不再发生交换或n轮冒泡后则排序成功。

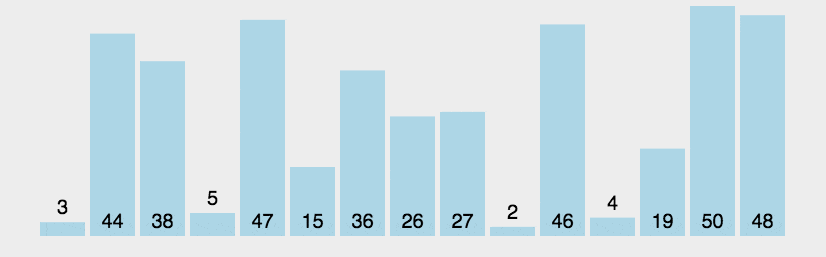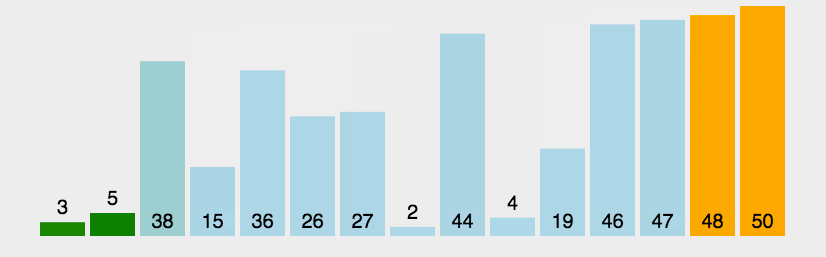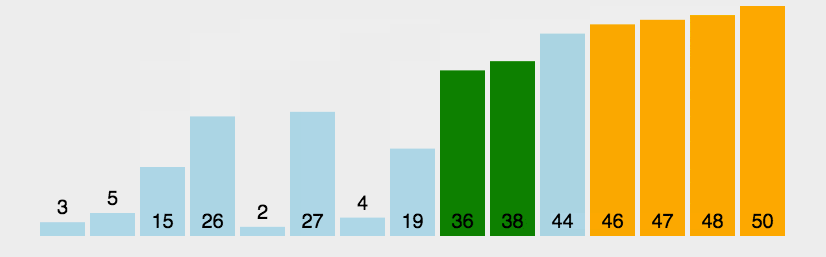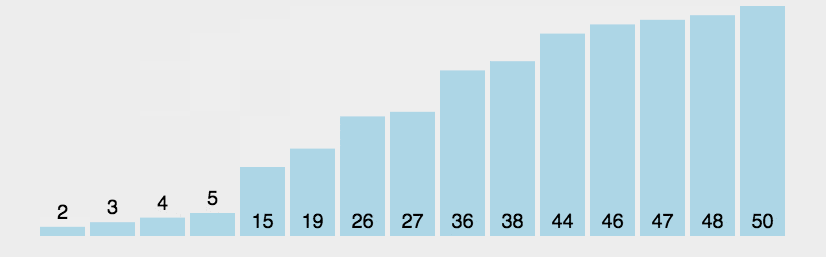
  • 实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    def bubble_sort(A):
        n = len(A)
        for i in xrange(n-1,0,-1):
            flag = False
            for j in xrange(i):
                if A[j] > A[j+1]:
                    A[j],A[j+1] = A[j+1],A[j]
                    flag = True
            if not flag:return

  • 分析

    • 时间复杂度：
      • 最好情况下，初始有序，只比较n-1次，交换0次，O(n)；
      • 最坏情况下，初始逆序，O(n^2)；
    • 空间复杂度：O(1)
    • 稳定性：相等两元素不进行交换，稳定

快速排序（quick sort）

  • 思想：基于分治和递归的思想，任选一个元素作为枢轴点，将所有小于等于它的元素都放在它前面，所有大于它的元素都放在后面，将枢轴点放在其最终位置，然后再递归排序枢轴点左右两侧子序列。
  • 基本实现思路：首元素作为枢轴点
    • ① 分解：
      • 选取A[0]作为枢轴值，将小于(等于)它的元素放在1~k，然后交换A[0]与A[k]，k是枢轴值最终位置
      • 过程使用口袋双指针法，j指针指向当前遍历位置(1~n-1)，i指针指向已存储的小于等于枢轴值的最后一个元素位置(1 ~ k)，如果A[j] <= A[0]就把A[j]与A[i+1]交换
    • ② 求解：递归求解0 ~ k-1，和k+1 ~ n-1子问题
  • 改进思路：随机快排，事实证明如果每次选取首元素作为枢轴点，很容易达到最坏情形，时间复杂度变为O(n^2)，改进思路也很简单，只需要在每次数组划分时随机选择一个元素与首元素进行交换，其余代码即可保持不变。实际使用的都是随机快排，因为首元素快排性能实在是太差了!!！以LeetCode 215题为例，是40ms与1000ms的差距。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import random
def partition1(A,low,high):
    """
    选取A[low:high+1]的首元素A[low]作为枢轴，通过口袋指针法对数组进行划分
    """
    bag = low                    
    for j in xrange(low+1,high+1): 
        if A[j] <= A[low]:
            bag += 1
            A[bag],A[j] = A[j],A[bag]
    A[bag],A[low] = A[low],A[bag]
    return bag
    
def partition2(A,low,high):
    """
    随机选取A[low:high+1]中的元素，与A[low]交换，再进行划分
    """
    rand = random.randint(low,high)
    A[rand],A[low] = A[low],A[rand]
    
    bag = low                    
    for j in xrange(low+1,high+1): 
        if A[j] <= A[low]:
            bag += 1
            A[bag],A[j] = A[j],A[bag]
    A[bag],A[low] = A[low],A[bag]
    return bag
    
def quicksort1(A,low,high):
    """
    原地+递归实现
    """
    if low < high:
        pivot = partition(A,low,high)
        quiksort(A,low,pivot-1) 
        quiksort(A,pivot+1,high)

def quicksort2(A,low,high):
    """
    原地+非递归实现：使用栈模拟递归过程
    """
    if low >= high:return 
    s = [[low,high]]
    while s:
        l,h = s.pop()
        pivot = partition(A,l,h) # 分解
        if pivot + 1 < h:s.append([pivot+1,h])
        if pivot - 1 > l:s.append([l,pivot-1])
                    
def quicksort(A):
    """
    非原地实现
    """
    n = len(A)
    if n < 2:
        return A
    rand = random.randint(0,n-1)
    A[0],A[rand] = A[rand], A[0]
    l = [x for x in A[1:] if x <= A[0]]
    r = [x for x in A[1:] if x > A[0]]
return quiksort(l) + [A[0]] + quiksort(r)

  • 分析：使用递归树来分析

    • 时间复杂度：递归深度×O(n)。递归深度和每次划分是否对称有关，最坏情况下初始有序或逆序，递归深度为n，时间复杂度为O(n^2)；最好情况下每次都进行均分，递归深度为lgn，时间复杂度为O(nlgn)；平均情况下，快排接近于最佳情况，为O(nlgn)。快速排序是内部排序中平均性能最好的排序算法。
    • 空间复杂度：递归深度,最坏O(n),最好O(lgn),平均O(lgn)
    • 稳定性：存在跨距交换，不稳定

  • 改进：

    • 规模较小时不再继续递归调用，采取直接插入排序
    • 合理选取枢轴点：每次随机选取枢轴点或取头、尾、中间的中间值(将其与首元素交换，这样就不用修改以上代码)，这样最坏情况在实际中就几乎不会发生了。

选择排序

每次从当前待排序列中选择最小元素将其交换到首位，n-1轮完成排序。

简单选择排序(selection sort)

  • 思路：每轮从A[i:]中选出最小元素与A[i]交换，i= 0…n-2
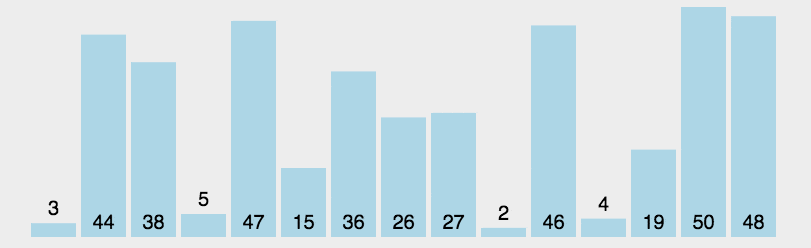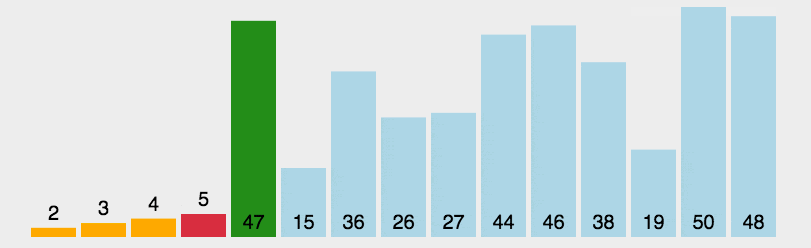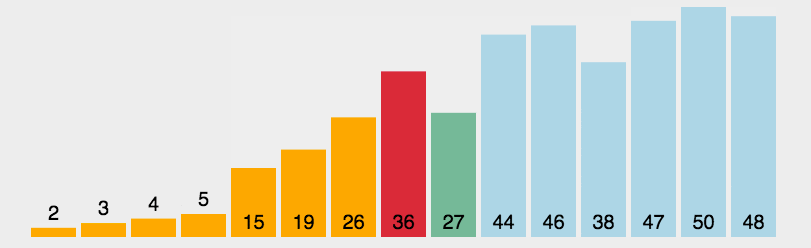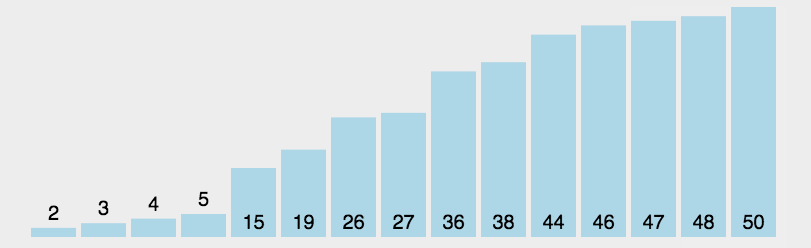
  • 实现：
1
2
3
4
5
6
7
def SelectSort(A):
    n = len(A)
    for i in xrange(n-1):
        min = i
        for j in xrange(i+1,n):
            if A[j] < A[i]:min = j
        A[i],A[min] = A[min],A[i]
  • 分析
    • 时间复杂度：元素移动次数最好情况是0，最坏情况是O(n)，元素比较次数和序列初始状态无关为n(n-1)/2;所以时间复杂度最好最坏都是O(n^2)
    • 空间复杂度：O(1)
    • 稳定性：存在跨距交换，不稳定

堆排序(heap sort)

  • 堆的定义：序列A[1,2…n]被称为堆，当且仅当该序列满足

    • ① $A[i] <= A[2i]$ 且 $A[i] <= A[2i+1]，i\in [1,n//2]$,小根堆
    • ② $A[i] >= A[2i]$ 且 $A[i] >= A[2i+1]，i\in [1,n//2]$,大根堆

  • 堆与完全二叉树：将序列A看做是一颗完全二叉树，树的根节点是A[1]，给定一个节点的下标i，A[i/2]是它的父亲节点，A[2i]是它的左孩子，A[2i+1]是它的右孩子

向下调整算法

向下调整算法:假设节点i的左右子树已是大根堆，向下调整i节点以使以i为根的子树也成为大根堆

  1. 找到左右孩子中最大的，与父亲比较
  2. 如果大于父亲，则父亲与孩子中较大的交换，然后递归向下调整较大子节点
  3. 如果不大于父亲，则说明以i为根的子树已经是大根堆了
1
2
3
4
5
6
7
8
9
10
11
12
# 堆以下标1开始，0分量可用于存储当前堆长度heap-size
def heapify(A,i,n):
    # i:将元素i向下调整
    # n:当前堆中元素个数
    l,r = 2*i,2*i+1
    if l <= n:
        largest = r if l<n and A[r] > A[l] else l
    else:
        largest = i
    if A[i] != A[largest]:
        A[i],A[largest] = A[largest],A[i]
        heapify(A,largest,n)

分析：时间复杂度：O(h),h为堆的高度

建堆

从n/2到1，依次向下调整节点

1
2
3
4
def Build_max_heap(A):
    A[0] = len(A)-1 # 使用A[0]存储当前堆容量
    for i in xrange(A[0]//2,0,-1):
        heapify(A,i,A[0])

分析：建堆的时间复杂度为O(n)

堆排序

堆排序:每轮交换堆顶和堆底元素，将堆长度减1，堆顶向下调整，n-1轮后堆中只剩一个元素，排序完成。

1
2
3
4
5
def heapsort(A):
    build_max_heap(A) # 构建堆
    for i in xrange(len(A)-1,0,-1): # 堆排序：交换堆顶和堆底，堆长度-1，向下调整堆顶
        A[1],A[i] = A[i],A[1]
        heapify(A,1,i-1)
  • 分析：
    • 时间复杂度：建堆过程花费O(n)，每次向下调整花费O(lgn)，排序过程需要交换、调整n-1次，所以堆排序时间复杂度为O(nlgn)
    • 空间复杂度：O(1)
    • 稳定性：不稳定

归并排序(merge sort)

  • 思路：二路归并排序基于分治和递归的思想，首先将序列分解为左右两个子序列，分别对左右子序列进行归并排序，再归并左右两个已排序序列
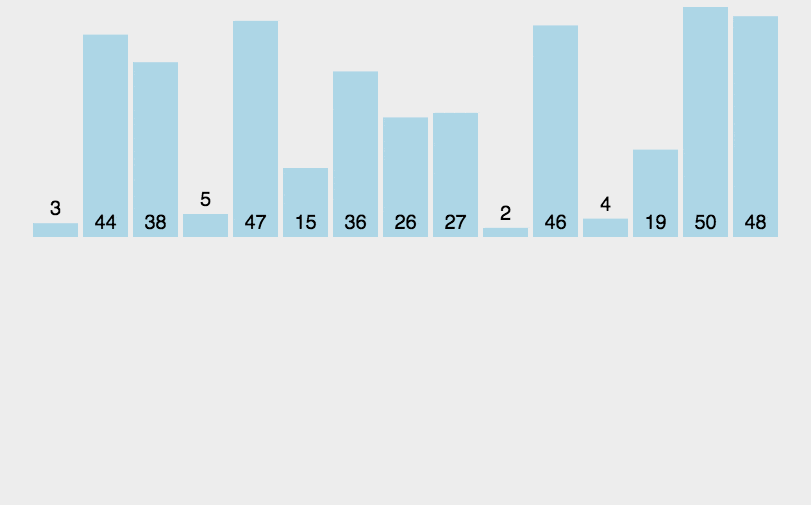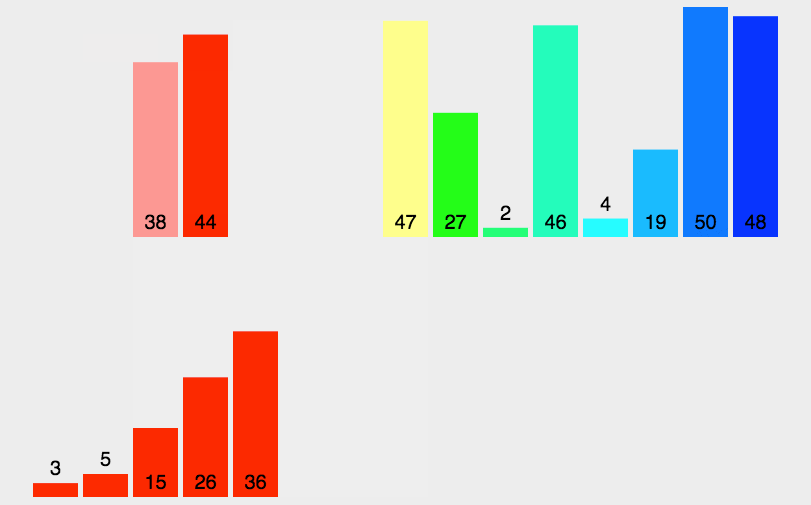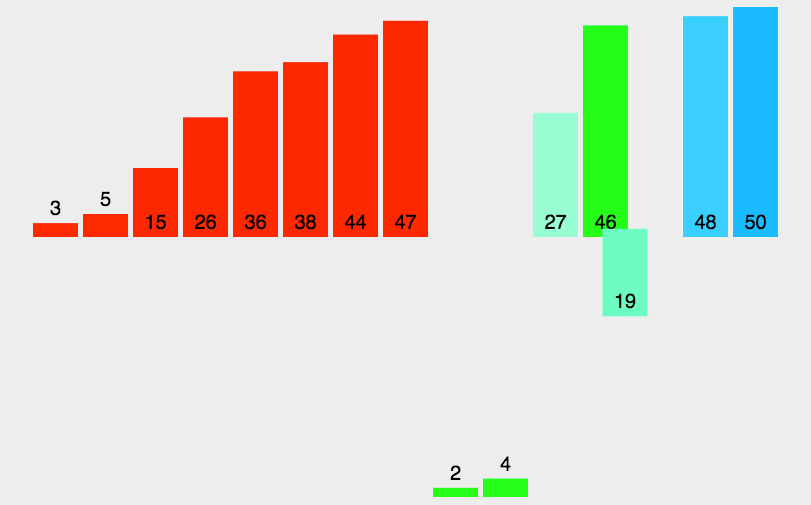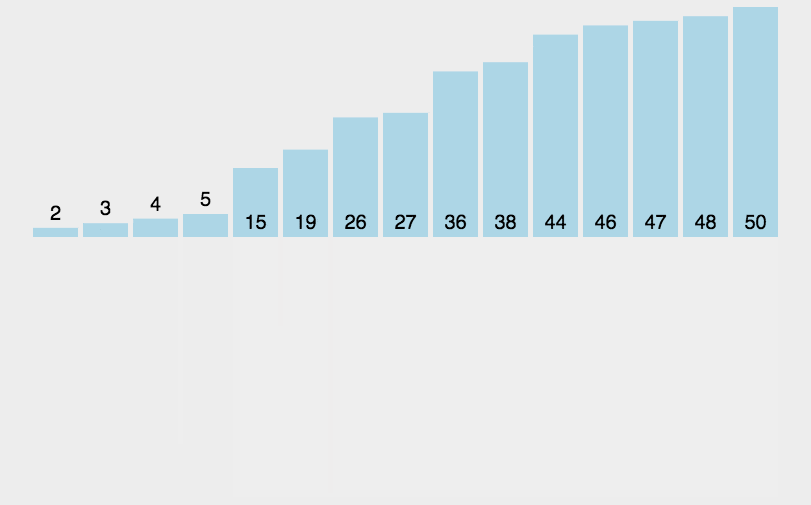
  • 实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def merge_sort(A,low,high):
    if low < high:
        mid = (low+high)/2 # 分解
        merge_sort(A,low,mid) # 解决
        merge_sort(A,mid+1,high)
        merge(A,low,mid,high) # 合并

def merge(A,low,mid,high):
    i,j,k=low,mid+1,low
    B = A[:] # 使用辅助数组B对A进行备份
    while i<=mid and j<=high:
        if B[i] < B[j]: # 比较左右序列，将小的放入B
            A[k] = B[i]
            i += 1
        else:
            A[k] = B[j]
            j += 1
        k += 1
    if i <= mid:A[k:high+1]=B[i:mid+1] # 前半段还有剩余，则直接添加到k后面
    if j <= high:A[k:high+1]=B[j:high+1]
  • 分析
    • 时间复杂度：一趟归并需要O(n)，总共需要lgn趟归并，所以算法时间复杂度为O(nlgn)
    • 空间复杂度：merge操作中，辅助空间刚好占用n个单元，O(n)
    • 稳定性：merge操作不会改变相同关键字的顺序，稳定

基数排序(Radix sort)

  • 概念：三围n、d、r
    • n：待排序序列中节点个数（有多少个待排序数字）
    • d：每个节点所包含的关键字个数（每个数最大位数）
    • r：基数，每个关键字有多少种取值（桶个数）
    • 低位优先排序（LSD）：从低位开始排序
    • 高位优先排序（马上到！）：从高位开始排序
  • 思路：低位优先排序，从低位到高位需进行d轮排序，每轮排序包括了分配和收集两个过程：
    • 分配：按照各节点在该位上的关键字值将其分配到对应的队列中去
    • 收集：将各队列中的节点依次首尾相连，得到新的节点序列
  • 实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
def radix_sort(A):
    """A为正整数序列"""
    r = 10 # 基数为10
    d = len(str(max(A))) # 整数最大位数
    bucket = [[] for i in xrange(r)] # 初始化十个队列
    for i in xrange(d): # 需要d轮分配、组合
        # 分配：如果整数这一位是i，则将其分配到bucket[i]
        for num in A:bucket[num%(r**(i+1))/(r**i)].append(num)
        # 收集：
        del A[:]
        for q in bucket:
            A.extend(q)
        bucket = [[] for i in xrange(r)]
  • 分析：
    • 时间复杂度： 总共需d轮分配收集，每趟分配需O(n)，收集需O(r)，O(d(n+r))
    • 空间复杂度：需要r个队列，O(r)
    • 稳定性：对基数排序而言很重要一点就是按位排序时必须是稳定的

桶排序

  • 思路：分桶-桶内排序-收集
    1. 假设待排序的一组数统一的分布在一个范围中，并将这一范围划分成几个子范围，也就是桶;
    2. 将待排序的一组数，分档规入这些子桶，并将桶中的数据进行排序;
    3. 将各个桶中的数据有序的合并起来;
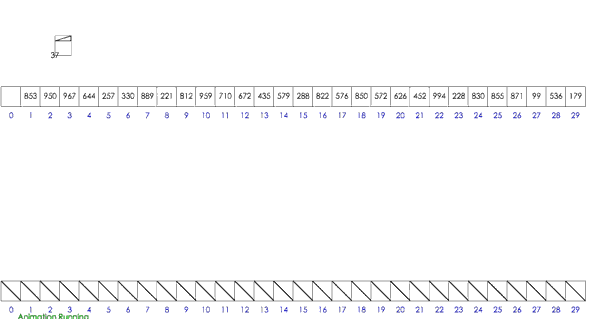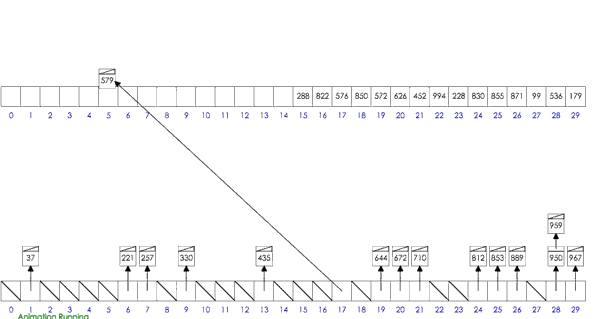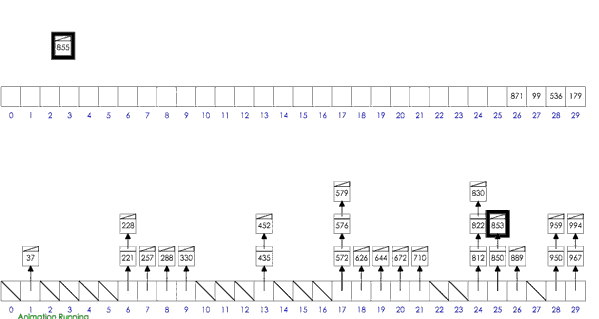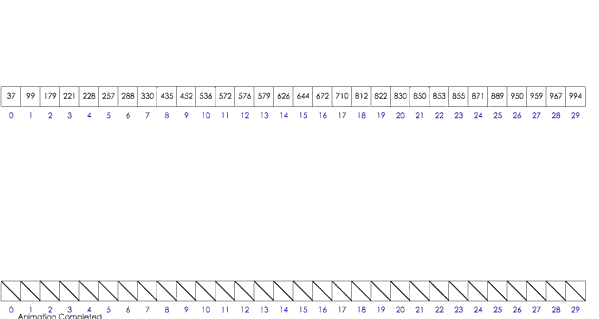
  • 分析：桶排序的平均时间复杂度为线性的O(N+C)，其中C=N*(logN-logM)。如果相对于同样的N，桶数量M越大，其效率越高，最好的时间复杂度达到O(N)。 当然桶排序的空间复杂度 为O(N+M)，如果输入数据非常庞大，而桶的数量也非常多，则空间代价无疑是昂贵的

常见排序算法比较

参考

坚持原创技术分享，您的支持将鼓励我继续创作！