数据结构与算法：并查集

发表于 | 更新于: | 分类于 | 阅读次数:
字数统计: 6.5k | 阅读时长 ≈ 28

理论篇

动态连通性问题

假设用 0~N-1 的整数来表示一组对象，整数对(p,q)可以理解为“对象p和对象q是相连的”，相连是一种对等关系，意味着：

  1. 自反性：p和p是相连的；
  2. 对称性：p和q相连那么q和p也相连；
  3. 传递性：p和q相连，q和r相连，则p和r也是相连的；

对等关系能够将对象分为多个等价类，当且仅当两个对象相连时它们才属于同一个等价类。动态连通性问题或说等价类划分问题需要设计一种数据结构来保存所有对象间的连通/等价关系，并用它来判断一对新的对象是否是连通/等价的。

逻辑结构

并查集（Union Find Set）是解决动态连通性问题的一种非常高效的树型数据结构，并查集是由一组树构成的森林，每棵树都描述了一个等价类，树中所有节点都是相连的。

称谓 整数 整数对 相连的整数 标识符
集合观点 元素 是否属于同一集合 等价类 集合名
树的观点 节点 是否连通 连通分量/树 根节点

存储结构

通常用树的双亲表示法作为并查集的存储结构，这种存储方式采用一组连续的空间来存储每个节点，同时在每个节点中增设一个伪指针，指示其双亲节点在数组中的下标。通常用数组元素的下标代表元素名，根节点的下标代表集合名，根节点的双亲节点为其本身或负数。

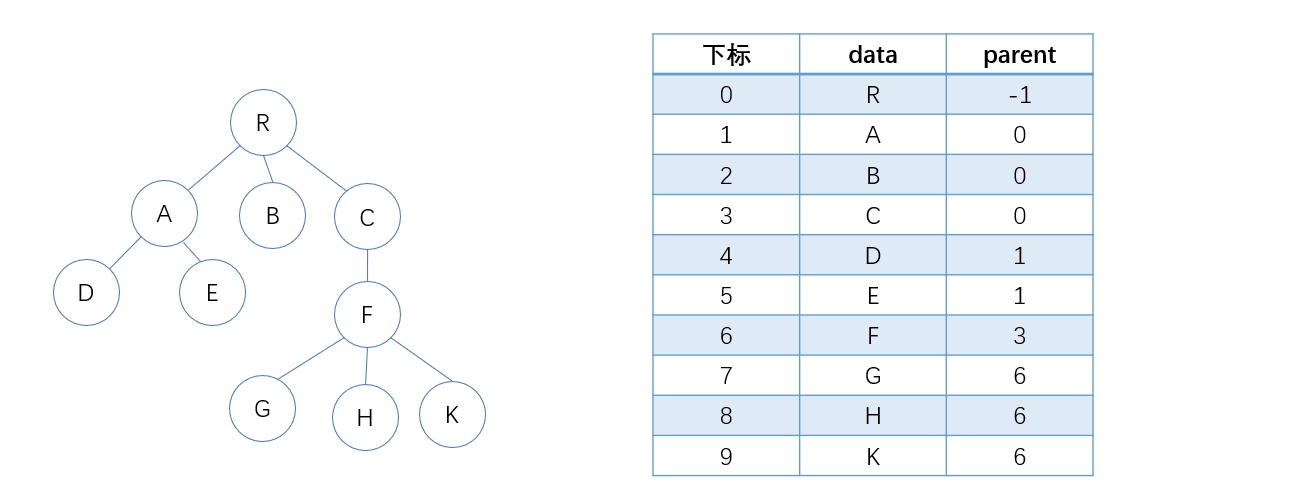
基本运算

运算定义

Union-Find算法API定义（图论语言描述）:

  1. uf(int n)：用整数标识(0~N-1)初始化N个节点，每个节点单独构成一个连通分量；
  2. int find(int p)：查找节点p所在分量的标识符；
  3. void union(int p,int q)：如果p和q在不同分量，union会融合两个分量；
  4. bool connected(int p,int q)：如果p和q存在于同一分量则返回True；
  5. int count()：连通分量的数量；

运算实现

1）quick-find 实现

find 的时间复杂度取决于树的高度，因此为了加快find的速度需要在合并两个分量时尽量减小合并后树的高度，一种方式是在每次合并不同分量时，统一分量的标识符，这种方式虽然使find时间复杂度变为O(1)，但union时需要表里整个数组，对于大量数据并不适用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Uf(object):
    def __init__(self, n):
        """用一个数组来存储并查集，初始化时每个节点的分量标签是其自身id"""
        self.id = [for i in range(n)]
        self.count = n
    def find(self, p):
        """查找p节点的分量标签，即根节点id"""
        while p != self.id[p]:
            p = self.id[p]
        return p
    def union(self,p,q):
        """如果p和q不在同一分量，则合并这两个分量，同时统一分量的标识符"""
        p_id = self.find(p)
        q_id = self.find(q)
        if p_id != q_id:
            for i in range(len(self.id)):
                if self.id[i] == q_id:
                    self.id[i] = p_id
            self.count -= 1
    def connectd(self,p,q):
        """判断p和q是否在同一分量"""
        return self.find(p) == self.find(q)
    def count():
        """统计连通分量个数"""
        return self.count

分析:

  1. find:所有节点的父节点就是根节点，$O(1)$
  2. union:$O(n)$
  3. 处理N对整数，$O(n^2)$
2）quick-union 实现

quick-union不去统一union的两个分量的标识符，通过链式追溯找到节点的标识符。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Uf(object):
    def __init__(self, n):
        """用一个数组来存储并查集，初始化时每个节点的分量标签是其自身"""
        self.id = [for i in range(n)]
        self.count = n
    
    def find(self, p):
        """查找p节点的分量标签，即根节点id"""
        while p != self.id[p]:
            p = self.id[p]
        return p
    def union(self,p,q):
        """如果p和q不在同一分量，则合并这两个分量"""
        p_id = self.find(p)
        q_id = self.find(q)
        if p_id != q_id:
            self.id[q_id] = p_id
            self.count -= 1
            
    def connectd(self,p,q):
        """判断p和q是否在同一分量"""
        return self.find(p) == self.find(q)
    def count():
        """统计连通分量个数"""
        return self.count

分析：

  1. find：比较次数等于树的高度，最坏情况下O(n)；
  2. union：两次find，树的高度O(n)
  3. 处理N对整数所需的所有find()操作访问数组的总次数在最坏情况下是平方级别的
3）终极优化——带路径压缩的加权 quick-union

find操作是整个并查集操作的核心，要加快find操作效率需尽量减小树的高度（扁平化），我们可以在find或union操作时实现这一点：

  1. 路径压缩：在find的同时将节点直接链接到根节点；
  2. 加权quick-union：在union时总是将较小子树链接到较大子树；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Uf(object):
    def __init__(self, n):
        """用一个数组来存储并查集，初始化时每个节点的分量标签是其自身"""
        self.id = [for i in range(n)]
        # 统计连通分量个数
        self.count = n
        # 统计分量中节点个数
        self.rank = [1] * n    
    def find(self, p):
        """查找p节点的分量标签，即根节点id，同时将路径上的所有节点的父节点设置为根节点"""
        while p != self.id[p]:
            self.id[p] = find(self.id[p])
            p = self.id[p]
        return p
    def union(self,p,q):
        """如果p和q不在同一分量，则将小分量合并到大分量"""
        x, y = self.find(p), self.find(q)
        if x != y:
            if self.rank[x] > self.rank[y]:
                self.id[y] = x
                self.rank[x] += self.rank[y]
            else:
                self.id[x] = y   
                self.rank[y] += self.rank[x]       
            self.count -= 1
            
    def connectd(self,p,q):
        """判断p和q是否在同一分量"""
        return self.find(p) == self.find(q)
    def component_count(self):
        """统计连通分量个数"""
        return self.count
    def node_count(self):
        """统计每个分量中节点个数"""
        return {self.find(i):self.rank[i] for i in self.id}

示例：依次添加[(1,2),(3,4),(0,9),(4,7),(6,5),(5,8),(3,9),(1,8)]的过程

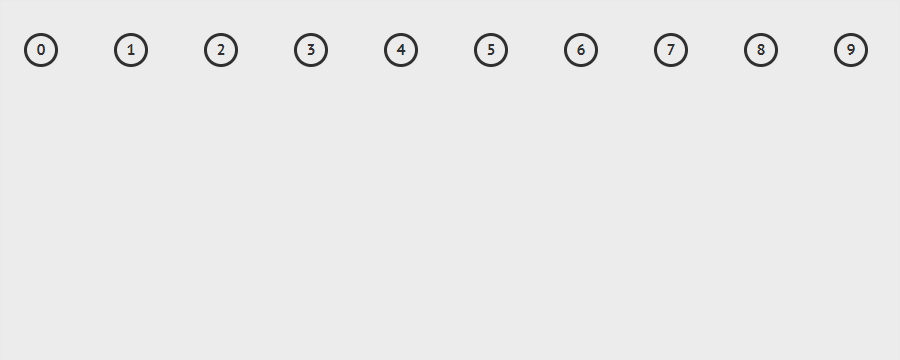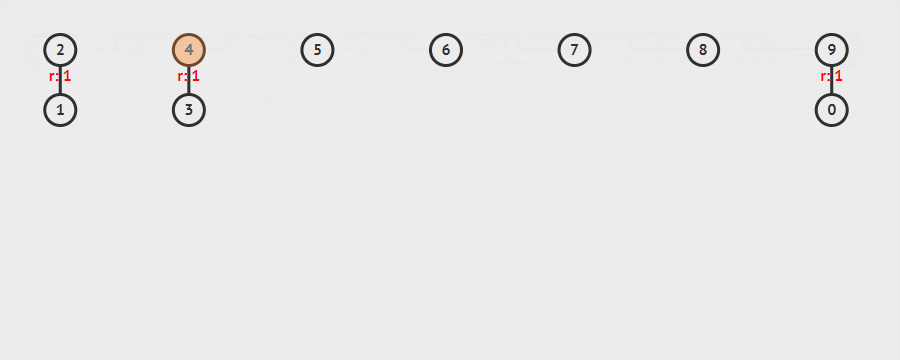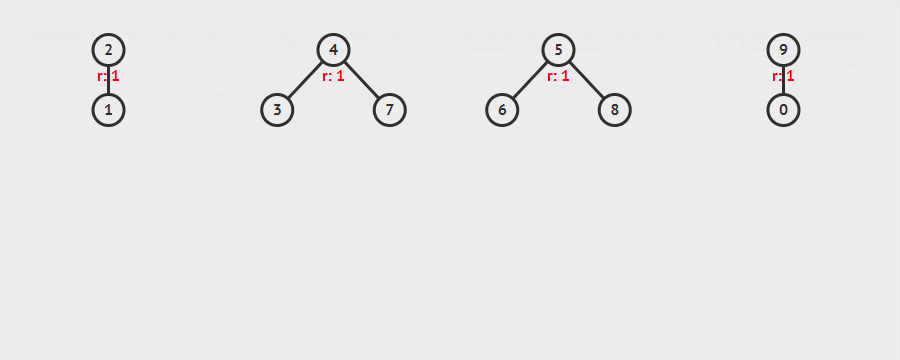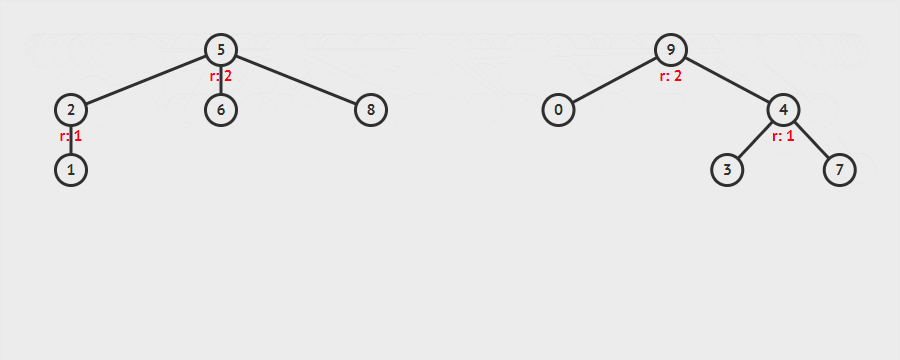
分析：同时使用路径压缩、按秩（rank）合并优化的程序每个操作的平均时间仅为 $O(\alpha (n))$，其中 $ \alpha (n)$ 是 $ {\displaystyle n=f(x)=A(x,x)}$ 的反函数， ${\displaystyle A}$ 是急速增加的阿克曼函数。因为 $\alpha (n)$ 是其反函数，故 $ \alpha (n) $在 n 十分巨大时还是小于 5。因此，平均运行时间是一个极小的常数。实际上，这是渐近最优算法：Fredman 和 Saks 在 1989 年解释了 $ \Omega (\alpha (n))$ 的平均时间内可以获得任何并查集。

  1. find:均摊成本接近O(1)；
  2. union:均摊成本接近O(1)；
  3. 保存所有连接关系:O(n)，n为边的个数;
  4. 空间复杂度O(n)；
  5. 带路径压缩的加权quick-union算法是最优的算法，但并非所有操作都能在常数时间内完成；
  6. 值得注意的是，路径压缩并不能保证最终所有节点都能直接作为根节点的孩子节点，除非最后对每个节点都find一遍。find过程确实将路径上的所有节点都放在了根节点下，但是Union过程会破坏这一点，导致最终的树高度变得未知。因此加权quick-union效率会更高，而且统计了每个分量中节点个数。
  7. 加权quick-union已经使得树变得很低，进一步的路径压缩很难再对其进一步改进了。

quick-union和加权quick-union算法对比：

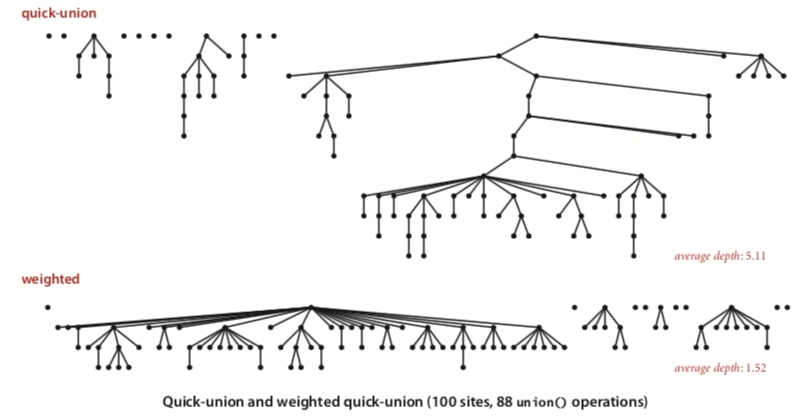
三种算法性能对比：

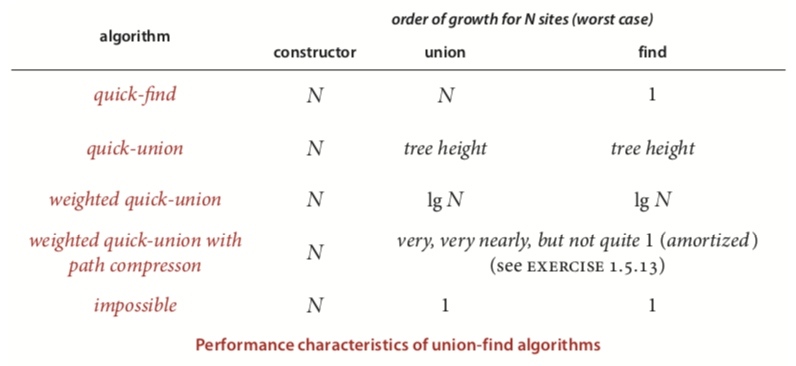
三种算法均摊成本对比（灰色点代表累积成本，红色点代表均摊成本）：

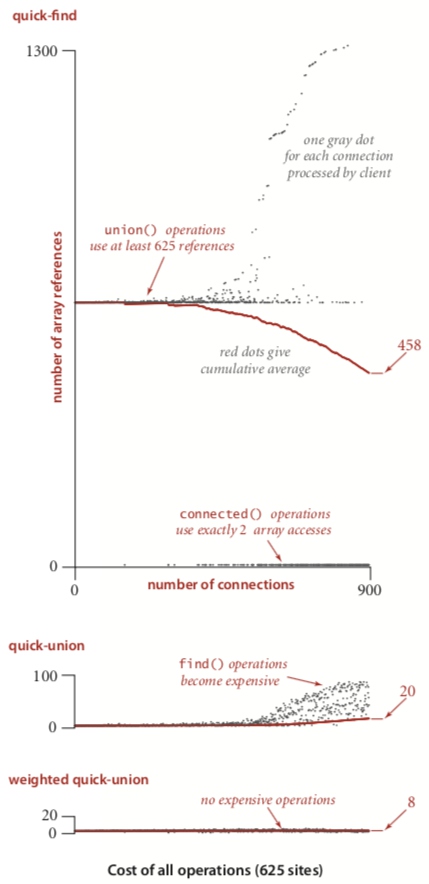
关于并查集更详细内容，Algorithms一书的Section 1.5有非常精彩的讨论。

典型应用

划分等价类

  • 问题：给定一组对象的对等关系，对该组对象进行划分，使得具有对等关系的对象归为一类；
  • 思路：典型的等价类划分问题，遍历所有对等关系，union两个节点，即完成了等价类的划分；
1
2
3
4
5
6
7
8
9
10
11
def eq_class(vertices,edges):
    n = len(vertices)
    uf = Uf(len(vertices))
    for p,q in uf:
        if uf.find(p) != uf.find(q): 
            uf.union(p,q)   
    res = {}
    for i in range(n):
        res[uf.find(i)] = res.get(uf.find(i),[]) + [i]
    return res

Kruskal算法

  • 问题：寻找带权图的最小生成树
  • 思路：贪心策略，从小到大依次选取不构成环的边，直至所有顶点都被纳入
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def kruskal(graph):
    """
    graph = {node:[(node1,weight1),...]}
    """
    # 构建并查集
    vertices = graph.keys()
    n = len(vertices)
    uf = Uf(n)
    
    # 维护边的优先队列
    edges = []
    for key in graph:
        edge = [graph[key][1],(key,graph[key][0])]
        heappush(edges,edge)
    
    # kruskal算法
    T = []
    while n > 1:
        i,j = heappop(edges)[1]
        if uf.find(i) != uf.find(j):
            uf.union(i,j)
            T.append([i,j])
        else:
            continue    
    return T
  • 分析：采用优先队列存放边的集合，每次选取最小权值的边需$O(lg|E|)$，每次使用并查集判断是否构成环需$O(1)$，最坏情形需要遍历所有边，所以时间复杂度为$O(|E|lg|E|)$。

实战篇

实战技巧

  1. 实战的难点在于问题的定义和转化，是否可以转化为对象间连通性的讨论
    1. 抽象出节点：节点代表了某种相互联系的对象
    2. 抽象出节点之间的边：代表了节点之间的某种等价性
  2. “动态连通问题”的衍生问题包括：
    1. 判断两个节点是否连通：判断两个节点是否属于同一类
    2. 添加一组新的连通关系
    3. 统计等价类、连通分量个数，每个等价类中的节点数
  3. 并查集的实现：
    1. 节点用整数来指示，我们可以将对象存储在一个数组中，通过其下标来指示该对象
    2. 建议使用带路径压缩的quick-union，代码简单，性能最优
    3. 在节点合并时，需要遍历所有边，输入可以是边表或邻接表，时间复杂度为边的个数
  4. 并查集能解决的问题通过DFS也都能解决

    2.2 经典LeetCode题目

    [684.medium] 识别无向图中的冗余边

  • 问题：给定含n个节点的无向图（用边表表示），该图由一棵树和一条多余边构成，返回一条可以删去的边，如果有多个答案则返回最后出现的那条边。
1
2
3
4
5
6
输入: [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]
解释: 给定的无向图为:
5 - 1 - 2
    |   |
    4 - 3
  • 思路：无向图中冗余边必定构成环，只需要识别出无向图的环，从环中去掉最后一条边即可。构建n个节点的并查集，依次合并边表中的边的两个顶点，如果在合并时发现这两个顶点在并查集中连通，则说明该边是多余的，返回该边；
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution(object):
    """
    思路：典型的并查集应用，从一系列边中找出生成树的冗余边
    """
    def findRedundantConnection(self, edges):
        """
        :type edges: List[List[int]]
        :rtype: List[int]
        """
        def init_uf(n):
            return [i for i in range(n)]
            
        def find(a,i):
            while a[i] != i:
                a[i] = find(a,a[i])
                i = a[i]
            return i
        
        def union(a,i,j):
            a[find(a,j)] = a[find(a,i)]
            return a
        
        n = len(edges)
        uf = init_uf(n+1)
        for p,q in edges:
            if find(uf,p) == find(uf,q):
                return [p,q]
            else:
                union(uf,p,q)

[685.hard] 识别有向图中的冗余边

  • 问题：将问题684中的无向图换做有向图，问题不变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
输入: [[1,2], [2,3], [3,4], [4,1], [1,5]]
输出: [4,1]
解释: 给定的有向图如下:
5 <- 1 -> 2
     ^    |
     |    v
     4 <- 3
 
输入: [[1,2], [1,3], [2,3]]
输出: [2,3]
解释: 给定的有向图如下:
  1
 / \
v   v
2-->3
  • 思路：有向图的冗余边情况稍复杂一些，需分三种情况讨论。

1）如果所有节点最多都只有一个父亲：则必在根节点处形成环，只需返回最后一个成环的边即可（类似于无环题）
2）如果某节点由两个父亲，但该节点未形成环，则返回两个父亲最后一条边；
3）如果某节点由两个父亲，且该节点在环中，则需返回在环中的那条父亲边；

  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution(object):
    def findRedundantDirectedConnection(self, edges):
        """
        :type edges: List[List[int]]
        :rtype: List[int]
        """
        def find(a):
            # 返回a的根节点，即a的类
            while uf[a] != a:
                a = uf[a]
            return a
        
        def union(a,b):
            # a祖先作为b祖先的父亲
            uf[find(b)] = find(a)
            
        def cycle_edge(x):
            # 返回环中边，无环返回None
            visited[x] = True
            for i in adj[x]:
                if visited[i]:
                    return x,i
                else:
                    tmp = cycle_edge(i)
                    if tmp:return tmp
            return None
            
        n = len(edges)
        uf = range(n+1)
        adj = [[] for i in range(n+1)]
        has_father = [False] * (n+1)
        edge_d = None
        visited = [0] * (n+1)
        
        for u,v in edges:
            adj[u] += [v]
            if has_father[v]:
                edge_d = (u,v)
            has_father[v] = True
            
            if find(u) == find(v):
                edge_c = (u,v)
            union(u,v)
        
        if not edge_d:
            return edge_c
        else:
            res = cycle_edge(edge_d[1])
            return res if res else edge_d

[547.medium] 朋友圈

  • 问题：班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
1
2
3
4
5
6
7
输入: 
[[1,1,0],
 [1,1,0],
 [0,0,1]]
输出: 2 
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。

  • 思路:每名学生作为一个节点，朋友关系作为边（传递性-对称性），构建并查集，统计并查集中联通分量的个数

  • 代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution(object):
    def findCircleNum(self, M):
        """
        :type M: List[List[int]]
        :rtype: int
        """
        n = len(M)
        edge = [(i,j) for i in range(n) for j in range(i+1,n) if M[i][j]]
        self.count = n
        
        def find(a,i):
            while i != a[i]:
                a[i] = find(a,a[i])
                i = a[i]
            return i
        
        def union(a,i,j):
            s,t = find(a,j),find(a,i)
            if s != t:
                a[s] = a[t]
                self.count -= 1
        
        uf = [i for i in range(n)]
        for i,j in edge:
            union(uf,i,j)
        return self.count

[200.medium] 岛屿的个数

  • 问题：给定一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围
1
2
3
4
5
6
7
输入:
11000
11000
00100
00011

输出: 3
  • 思路：并查集求连通分量个数；增加哑结点存放所有无关节点’0’，相连关系具有传递性，因此只需要向上和向左合并节点即可；
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution(object):
    def numIslands(self, grid):
        """
        :type grid: List[List[str]]
        :rtype: int
        """
        # 定义并查集操作
        def find(uf,p):
            while p != uf[p]:
                uf[p] = find(uf,uf[p])
                p = uf[p]
            return p
        def union(uf,p,q):
            x,y = find(uf,p),find(uf,q)
            if x != y:
                if self.rank[x] > self.rank[y]:
                    uf[y] = uf[x]
                    self.rank[x] += self.rank[y]
                else:
                    uf[x] = uf[y]
                    self.rank[y] += self.rank[x]
                self.count -= 1
        
        if not any(grid):
            return 0
        # 创建并查集，使用m*n哑元存放0分量
        m,n = len(grid), len(grid[0])
        total = m * n
        self.count = m*n
        self.rank = [1] * (total+1)
        uf = [i for i in range(total+1)]
        # 保存所有相连关系
        for i in range(m):
            for j in range(n):
                if grid[i][j] == '0':
                    union(uf,total,i*n+j)
                else:
                    if i > 0 and grid[i-1][j]=='1':
                        union(uf,(i-1)*n+j,i*n+j)
                    if j > 0 and grid[i][j-1]=='1':
                        union(uf,i*n+j-1,i*n+j)
        
        return self.count
  • 分析：
    • 时间复杂度：保存所有相连关系花费O(m*n)
    • 空间复杂度：O(m*n)

[765.hard] 情侣牵手

  • 问题：N 对情侣坐在连续排列的 2N 个座位上，想要牵到对方的手，计算最少交换座位的次数，以便每对情侣可以并肩坐在一起。人和座位用 0 到 2N-1 的整数表示，情侣们按顺序编号，第一对是 (0, 1)，第二对是 (2, 3)，以此类推
1
2
3
输入: row = [0, 2, 1, 3]
输出: 1
解释: 我们只需要交换row[1]和row[2]的位置即可。
  • 思路:将每对情侣看做一个节点并编号0~N-1，其中(2i,2i+1)是编号为i的两位情侣，如果初始时2j和2j+1位置坐着来自不同情侣u=row[2j]/2和v=row[2j+1]/2的两个人，则认为u节点和v节点是相连的，保存所有连通关系后，每个连通分量必定构成一个交换环，含有n个节点的交换环最少需要n-1次交换可将交换环拆解为n个自环，即所有情侣相遇，故总共需要的交换次数为sum(n-1)=N-k，k代表并查集中的连通分量个数。
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution(object):
    def minSwapsCouples(self, row):
        """
        :type row: List[int]
        :rtype: int
        """
        def find(uf,i):
            while i != uf[i]:
                uf[i] = find(uf,uf[i])
                i = uf[i]
            return i
        def union(uf,i,j):
            x,y = find(uf,j),find(uf,i)
            if x != y:
                uf[y] = uf[x]
                self.count -= 1
        
        n = len(row)/2
        uf = [i for i in range(n)]
        self.count = n
        for i in range(n):
            union(uf,row[2*i]/2,row[2*i+1]/2)
        return n - self.count
  • 分析：建立并查集保存所有连接关系需要O(n)

[130.medium] 被围绕的区域

  • 问题：给定一个二维的矩阵，包含 ‘X’ 和 ‘O’（字母 O），找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 ‘O’ 用 ‘X’ 填充
1
2
3
4
5
6
7
8
9
10
示例：
X X X X
X O O X
X X O X
X O X X
运行程序后，矩阵变为:
X X X X
X X X X
X X X X
X O X X
  • 思路：只需要判断哪些为O的元素不与边界的O连通。节点(i，j)可用整数in+j来指示，遍历所有O顶点，可以将边界的所有O节点合并到一个哑结点mn下，将O节点与左侧和上侧的O节点连通；最后判断不与哑结点相连的节点，改为X。
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution(object):
    def solve(self, board):
        """
        :type board: List[List[str]]
        :rtype: void Do not return anything, modify board in-place instead.
        """
        def find(uf,i):
            while i != uf[i]:
                uf[i] = find(uf,uf[i])
                i = uf[i]
            return i
        def union(uf,i,j):
            uf[find(uf,j)] = uf[find(uf,i)]
        def connected(uf,i,j):
            return find(uf,i) == find(uf,j)
        
        if not any(board):return
        m,n = len(board),len(board[0])
        uf = [i for i in range(m*n+1)]
        for i in range(m):
            for j in range(n):
                if board[i][j] == 'O':
                    index = i * n + j
                    if i == 0 or j == 0 or i == m-1 or j == n-1: union(uf,index, m*n)
                    if i > 0 and board[i-1][j] == 'O': union(uf,index,index-n)
                    if j > 0 and board[i][j-1] == 'O': union(uf,index,index-1)
                    
        for i in range(m):
            for j in range(n):
                if board[i][j] == 'O' and not connected(uf,i*n+j,m*n):
                    board[i][j] = 'X'

[721.medium] 账户合并

  • 问题：给定一个列表 accounts，每个元素 accounts[i] 是一个字符串列表，其中第一个元素 accounts[i][0] 是 名称 (name)，其余元素是 emails 表示该帐户的邮箱地址。如果两个帐户都有一些共同的邮件地址，则两个帐户必定属于同一个人，即使两个帐户具有相同的名称，它们也可能属于不同的人，因为人们可能具有相同的名称。一个人最初可以拥有任意数量的帐户，但其所有帐户都具有相同的名称。现在，我们想合并这些帐户，按以下格式返回帐户：每个帐户的第一个元素是名称，其余元素是按顺序排列的邮箱地址。accounts 本身可以以任意顺序返回。
1
2
3
4
5
6
7
8
Input: 
accounts = [["John", "johnsmith@mail.com", "john00@mail.com"], ["John", "johnnybravo@mail.com"], ["John", "johnsmith@mail.com", "john_newyork@mail.com"], ["Mary", "mary@mail.com"]]
Output: [["John", 'john00@mail.com', 'john_newyork@mail.com', 'johnsmith@mail.com'],  ["John", "johnnybravo@mail.com"], ["Mary", "mary@mail.com"]]
Explanation: 
  第一个和第三个 John 是同一个人，因为他们有共同的电子邮件 "johnsmith@mail.com"。 
  第二个 John 和 Mary 是不同的人，因为他们的电子邮件地址没有被其他帐户使用。
  我们可以以任何顺序返回这些列表，例如答案[['Mary'，'mary@mail.com']，['John'，'johnnybravo@mail.com']，
  ['John'，'john00@mail.com'，'john_newyork@mail.com'，'johnsmith@mail.com']]仍然会被接受
  • 思路：同一个account内的email具有连通关系（属于同一个人），只需要找到所有email的连通分量，绑定到对应的人输出即可。将email作为节点，同时存在于同一个acount的email具有连通关系，数组收集所有的email，使用其数组下标作为email的指示，构建并查集，可以得到属于不同人的连通分量，再由连通分量找到对应的email和人。在此过程，我们需要email到id，id到email，email到人的三种映射，我们使用三个hash表来建立它们的映射关系。
  • 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution(object):
    def accountsMerge(self, accounts):
        """
        :type accounts: List[List[str]]
        :rtype: List[List[str]]
        """
        # 由email到客户
        em = {email:account[0] for account in accounts for email in account[1:]}
        # 由id到email
        emails = list(em.keys())
        n = len(emails)
        # 由email到id
        em_id = {emails[i]:i for i in range(n)}
        
        def find(uf,i):
            while i != uf[i]:
                uf[i] = find(uf,uf[i])
                i = uf[i]
            return i
        def union(uf,i,j):
            uf[find(uf,j)] = uf[find(uf,i)]
        
        # 保存所有连通关系
        uf = [i for i in range(n)]
        for account in accounts:
            for j in range(2,len(account)):
                union(uf,em_id[account[j-1]],em_id[account[j]])
        
        # 每个连通分量的节点
        res = {}
        for i in range(n):
            res[find(uf,i)] = res.get(find(uf,i),[]) + [i]
        
        # 输出每个分量
        r = []
        for key in res:
            cur = [emails[i] for i in res[key]]
            cur = [em[cur[0]]] +sorted(cur)
            r.append(cur)
        return r
  • 分析：建立哈希表需要O(n)，n代表email个数，建立并查集需要O(n)，故总的时间复杂度为O(n)

[128.hard] 最长连续序列

  • 问题：给定一个未排序的整数数组，找出最长连续序列的长度，要求算法的时间复杂度为 O(n)。
1
2
3
输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。
  • 思路：节点表示nums数组下标，整数相邻代表他们之间相连，统计并查集中节点最多的连通分量，用rank记录以每个节点为根节点的子树节点树，求最大值
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution(object):
    def longestConsecutive(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        def find(uf,i):
            while i != uf[i]:
                uf[i] = uf[uf[i]]
                i = uf[i]
            return i
        def union(uf,i,j):
            x,y = find(uf,i),find(uf,j)
            if x != y:
                if self.rank[x] > self.rank[j]:
                    uf[y] = uf[x]
                    self.rank[y] += self.rank[x]
                else:
                    uf[x] = uf[y]
                    self.rank[y] += self.rank[x]

        if not nums:
            return 0
        n = len(nums)
        self.uf = [i for i in range(n)]
        self.rank = [1] * n
        dic = {}
        for i in xrange(n):
            # 忽略重复值
            if nums[i] in dic:continue
            dic[nums[i]] = i
            # 如果前面出现了与nums[i]相邻的元素则与其合并
            if nums[i] - 1 in dic:union(self.uf,i,dic[nums[i]-1])
            if nums[i] + 1 in dic:union(self.uf,i,dic[nums[i]+1])
        return max(self.rank)

[778.hard] Swim in Rising Water

  • 问题：给定长宽为N的二维方阵grid，记grid[x][y] = z表示当时刻t >= z时，x, y可达。在grid上的移动可以瞬间完成，求从0, 0出发，到达N - 1, N - 1的最短时刻
1
2
3
4
5
6
7
8
9
10
11
Input: [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
Output: 16
Explanation:
 0  1  2  3  4
24 23 22 21  5
12 13 14 15 16
11 17 18 19 20
10  9  8  7  6

The final route is marked in bold.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected
  • 思路：并查集+二分查找，判断连通性。本题是要找到最小限高使得(0,0)与(n-1,n-1)能够连通，连通性关于限高具有单调性，可以采用二分查找的思路，每次将问题规模减半；
  • 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution(object):
    def swimInWater(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        def find(uf,i):
            while i != uf[i]:
                uf[i] = find(uf,uf[i])
                i = uf[i]
            return i
        def union(uf,i,j):
            x,y = find(uf,i), find(uf,j)
            if x != y:
                if rank[x] > rank[y]:
                    uf[y] = x
                    rank[x] += rank[y]
                else:
                    uf[x] = y
                    rank[y] += rank[x]
        def connected(uf,i,j):
            return find(uf,i) == find(uf,j)
        
        def is_connected(uf, limit):
            for i in xrange(n):
                for j in xrange(n):
                    if grid[i][j] <= limit:
                        cur = i*n+j
                        if i > 0 and grid[i-1][j] <= limit: union(uf,cur-n,cur)
                        if j > 0 and grid[i][j-1] <= limit: union(uf,cur-1,cur)
            return connected(uf,0,n*n-1)
        
        n = len(grid)
        low,high = max(grid[0][0],grid[n-1][n-1]), n*n-1
        while low <= high:
            uf = [i for i in xrange(n*n)]
            rank = [1] * n * n
            mid = (low+high)/2
            if is_connected(uf,mid):
                high = mid - 1
            else:
                low = mid + 1
        return low
  • 分析:时间复杂度 $O(nlgn)$

参考

[1] Algorithms 一书的Section 1.5
[2] LeetCode 并查集

坚持原创技术分享，您的支持将鼓励我继续创作！