数据结构与算法：二分查找

发表于 | 更新于: | 分类于 | 阅读次数:
字数统计: 8.4k | 阅读时长 ≈ 36

理论篇

二分查找（binary search）又称折半查找（half-interval search），用于在有序数组中以 $O(lgn)$ 的时间复杂度快速查找元素。

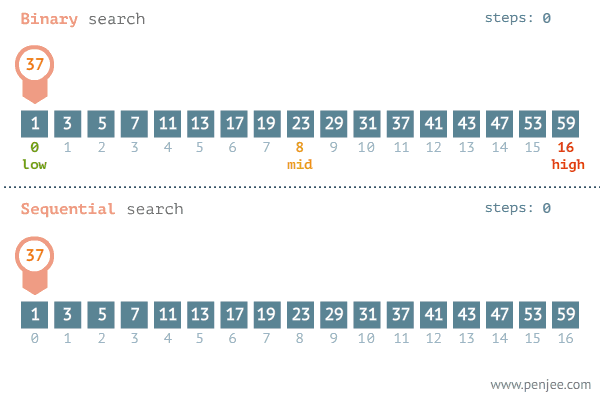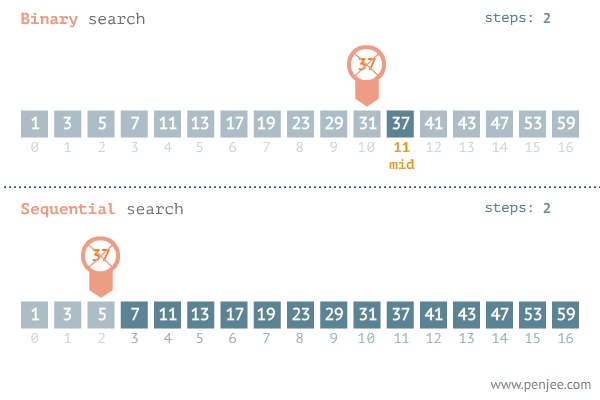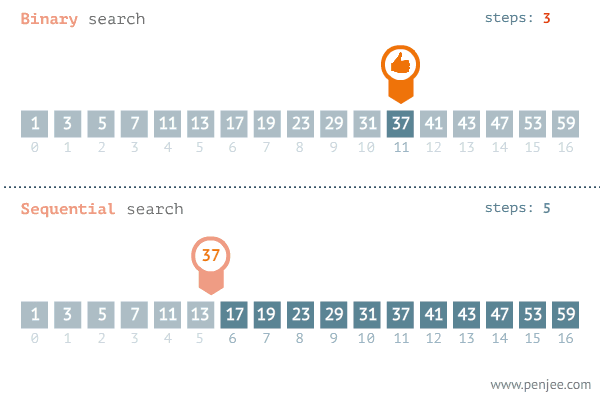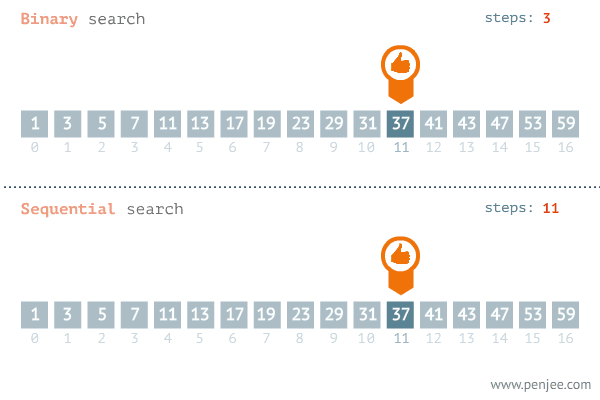
问题定义

二分查找算法所适用问题的形式化定义：在递增函数$f(x), x \in [l,r]$中, 由函数值y反向求取x。

  1. 递增函数 $f(x)$：$f(x)$ 表示由x计算y的一种函数映射，可以是非严格递增函数；
  2. x的定义域：x 的定义域标识初始化查找窗口；
  3. 问题变形：该问题常常演化为寻找第一个 $f(x)\geqslant y$ 的x，或者寻找第一个 $f(x)> y$ 的x；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 可将bisect统一理解为返回插入后的位置；
# bisect_left(a,x)返回a中第一个>=x的位置；
# bisect_right(a,x)返回a中第一个>x的位置；
# 如果没有查找到，bisect_left和bisect_right效果相同；
# 如果查找到，bisect_left返回a中第一个等于x的位置，bisect_right返回a中第一个大于x的位置；

bisect.bisect_left([1,2,2,3,3,4,4], 3)
3
bisect.bisect_right([1,2,2,3,3,4,4], 3)
5
bisect.bisect_left([1,2,2,3,3,4,4], 2.5)
3
bisect.bisect_right([1,2,2,3,3,4,4], 2.5)
3

一般原理

二分查找算法的一般框架：

  1. 初始化查找窗口：使用位置变量来表示当前查找窗口范围，可以使用闭区间表示$[l,r]$或开区间表示$[l,r)$
  2. 如果查找窗口不为空则循环以下过程：
    1. 在查找窗口内选取一个元素作为枢轴点，与目标值进行比较
    2. 如果目标值等于枢轴值，则返回枢轴点下标
    3. 如果目标值大于数轴值，则在枢轴点右侧窗口继续查找
    4. 如果目标值小于枢轴值，则在枢轴点左侧窗口继续查找
  3. 如果窗口为空仍未找到目标值，则返回目标值应插入位置的下标

说明：

  1. 查找区间表示：既可以使用闭区间也可以使用开区间，在代码实现上注意保证循环不变性以及最终返回值的含义；
  2. 枢轴值的选择：枢轴点原则上可以选取窗口内的任意元素，对枢轴值的不同选择可能会影响最终二分查找的效率；

代码实现

普通二分查找

闭区间二分查找

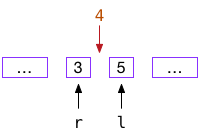
闭区间+下中位数是折半查找最清晰简便的实现，建议作为一般模板：

  1. 使用闭区间来初始化查找窗口：l=0,r=n-1，[l,r]表示初始化窗口；
  2. 如果窗口不为空则循环以下过程：窗口不为空即$l\leqslant r$
    1. 下中位数作为枢轴点：下中位数对应$ \frac{l+r}{2} $位置，上中位数对应$\frac{l+r+1}{2}$位置
    2. 如果目标值等于枢轴值，则返回数轴值下标
    3. 如果目标值大于数轴值，则在枢轴点右侧窗口继续查找
    4. 如果目标值小于枢轴值，则在枢轴点左侧窗口继续查找
  3. 如果未找到目标值，循环退出时l=r+1，目标值一定处于l和r之间；

1
2
3
4
5
6
7
8
9
10
11
12
# 闭区间写法:用[l,r]代表当前查找范围
def Binary_search(nums,key):
    l,r = 0,len(nums)-1 
    while l <= r:
        mid = (l + r) >> 1
        if key == nums[mid]:
            return mid
        elif key > nums[mid]:
            l = mid + 1
        else:
            r = mid - 1
    return l
半开区间二分查找

对窗口的描述方式变了，窗口初始化、退出条件都要做出相应修改，建议只作为参考。

1
2
3
4
5
6
7
8
9
10
11
12
# 开区间写法:用[l,r)代表当前查找范围
def Binary_search(nums,key):
    l,r = 0,len(L) 
    while l < r: 
        mid = (l + r) >> 1
        if key == nums[mid]:
            return mid
        elif key > nums[mid]:
            l = mid + 1
        else:
            r = mid 
    return l

结论：考虑思路的清晰性和结果的统一性，建议使用闭区间写法，本文以下讨论都是基于二分查找的闭区间写法。

含重复元素的二分查找

当数组中含有重复元素时，如果只需要返回任意一个与目标值相同的元素的下标，则上述代码无需变动，但如果需要查找目标值在数组中第一次/最后一次出现的位置，则需要对以上代码稍加改变即可。

接下来以“LeetCode 34. 在排序数组中查找元素的第一个和最后一个位置”为例，讨论两种方式。

等于作为小于/大于

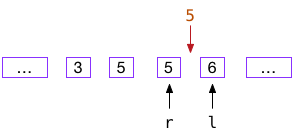
1、如果要寻找target第一次出现的位置，可以假装寻找$target-\varepsilon$，$\varepsilon$是一个大于0的很小的值，实际操作时可以把target==nums[mid]看做是小于，那么最终得到的l,r有以下关系，l=r+1

  1. 如果数组中存在目标值，nums[l]就是第一个等于target的元素；
  2. 如果数组中不存在目标值，nums[l]就是第一个大于target的元素；


2、如果要寻找target最后一次出现的位置，可以假装寻找$target+\varepsilon$，$\varepsilon$是一个大于0的很小的值，实际操作时可以把target==nums[mid]看做是大于，那么最终得到的l,r有以下关系，l=r+1

  1. 如果数组中存在目标值，nums[r]就是最后一个等于target的元素；
  2. 如果数组中不存在目标值，nums[r]就是最后一个小于target的元素；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def searchRange(self, nums, target):
    """
    :type nums: List[int]
    :type target: int
    :rtype: List[int]
    """
    # 寻找第一次出现的位置
    l,r = 0, len(nums) - 1
    L = R = -1
    while l <= r:
        mid = l + (r-l)/2
        if target <= nums[mid]:
            r = mid - 1
        else:
            l = mid + 1
    L = l
    
    # 寻找最后一次出现的位置
    l,r = 0, len(nums) - 1
    while l <= r:
        mid = l + (r-l)/2
        if target < nums[mid]:
            r = mid - 1
        else:
            l = mid + 1
    R = r
    # 如果L<=R说明存在目标值
    return [L,R] if L <= R else [-1,-1]
记录上一次成功位置

另一种方法对普通的二分查找的修改更少，只需要记录上次找到的位置，然后如果要找第一个就继续在左半部分找，如果要找最后一个就继续在右半部分继续找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 返回key在nums中第一次和最后一次出现的位置[L,R]，如果不存在则返回[-1,-1]
def searchRange(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        l,r = 0, len(nums) - 1
        L = -1
        while l <= r:
            mid = l + (r-l)/2
            if target == nums[mid]:
                L = mid
                r = mid - 1
            elif target < nums[mid]:
                r = mid - 1
            else:
                l = mid + 1
        
        l,r = 0, len(nums) - 1
        R = -1
        while l <= r:
            mid = l + (r-l)/2
            if target == nums[mid]:
                R = mid
                l = mid + 1
            elif target < nums[mid]:
                r = mid - 1
            else:
                l = mid + 1
        
        return [L,R]
  • 分析：
    • 最坏时间复杂度：O(lgn)
    • ASL ≈ lg(n+1)-1

二分查找的改进

折半查找每次选取中间元素作为枢轴点，插值查找和斐波那契查找通过改变枢轴点的选取方式对折半查找进行了改进。插值查找每次以插值的方式确定枢轴点，适合于元素关键字分布比较均匀的情况，斐波那契查找则是每次选取黄金分割点作为枢轴点。

插值查找

插值查找每次通过插值的方式来选取枢轴点：

  • 插值查找：mid = l + (r-l)*(key-L[l])/(L[r]-L[l])，其中L[r] != L[l],L[l] <= key <= L[r]

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    def insertion_search(L,key):
        l,r = 0,len(L)-1
        while l <= r:
            if key > L[r] or key < L[l]:return -1
            if L[r] == L[l]:return r
            mid = int(l + (r-l)*(key-L[l])/float((L[r]-L[l])))
            if key == L[mid]:
                return mid
            elif key > L[mid]:
                l = mid + 1
            else:
                r = mid - 1
        return -1

  • 分析：平均时间复杂度O(loglogN)，当关键字在数据集中分布较均匀时性能最好，当分布不均时可能比折半要差

斐波那契查找

  1. 找到大于F[k]-1 >= n的第一个k，在列表后面补充最后一个元素，使列表长度恰好为F[k]-1
  2. 选取mid = l+F[k-2]-1，恰好将列表分为左右F[k-2]-1和F[k-1]-1个元素
  3. 接下来和折半查找过程一致，只需判断相等时mid是否大于n-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
F = [0,1]
def Fibonacci(k):
    if k < len(F):
        return F[k]
    else:
        p = Fibonacci(k-1) + Fibonacci(k-2)
        F.append(p)
    return p

def Fibonacci_Search(L,key):
    n = len(L)
    k = 0
    while n > Fibonacci(k) - 1:
        k += 1
    
    L = L + L[-1:] * (F[k]-1-n)
    l,r = 0,n-1
    while l <= r:
        mid = l+ F[k-2] - 1
        if key == L[mid]:
            if mid >=n:
                return n-1
            else:
                return mid
        elif key > L[mid]:
            l = mid + 1
            k -= 1
        else:
            r = mid - 1
            k -= 2
    return -1
  • 分析：同样，斐波那契查找的时间复杂度还是O(log2n)，但是与折半查找相比，斐波那契查找的优点是它只涉及加法和减法运算，而不用除法，而除法比加减法要占用更多的时间，因此，斐波那契查找的运行时间理论上比折半查找小，但是还是得视具体情况而定

应用篇

应用二分查找算法解决实际问题的关键在于将问题抽象为“递增函数由y求x的问题”。具体地，应用二分查找算法分三步：

  1. 定义递增函数$f(x)$：明确递增函数的含义，x一般表示问题待求的值(如下标)，f(x)一般表示条件取值(如数组元素)；实现$f(x)$的计算过程(如数组索引取值)；值得说明的是，在定义出$f(x)$之后，并不需要将x所有定义域上的函数值全部求出，只需要计算每次选取的数轴点处的函数值即可(现取现用)；
  2. 确定$f(x)=k$时的定义域：一般可以通过函数值确定x的一个大致取值范围，该范围不必精确，只需保证包含x的确切解即可；
  3. 问题转化：将原始问题转化为在$f(x)$序列中寻找第一个大于(第一个大于等于、最后一个小于、最后一个小于等于)y的x的问题；

问题转化后即可套用二分查找的一般框架进行求解。

二分查找一般用于求解以下问题：

  1. 递增函数中查找某个值的问题：值作为y，下标作为x
  2. 递增函数中查找第k小问题：名次作为y，值作为x

数学问题

[LeetCode 69] 求x的平方根
  • 问题：实现 int sqrt(int x) 函数
  • 思路：f(x)=x**2，$x \in [1,x]$，在f(x)序列中查找最后一个<=target的x
  • 实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def mySqrt(self, x):
    """
    :type x: int
    :rtype: int
    """
    l, r = 0, x
    while l <= r:
        mid = (l+r) >> 1
        cur = mid * mid
        if x == cur:
            return mid
        elif x < cur: 
            r = mid - 1
        else:
            l = mid + 1
    return r
[LeetCode 367] 有效的完全平方数
  • 问题：给定一个正整数 num，编写一个函数，如果 num 是一个完全平方数，则返回 True，否则返回 False
  • 思路：单调函数f(i) = i*i，f(x)=val，x in [0,num]，是否能找到
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def isPerfectSquare(self, num):
    """
    :type num: int
    :rtype: bool
    """
    l,r = 0, num
    while l <= r:
        mid = (l+r)/2
        cur = mid * mid
        if cur == num:
            return True
        elif cur < num:
            l = mid + 1
        else:
            r = mid - 1
    return False
[LeetCode 668] 乘法表中第k小的数
  • 问题：给定高度m 、宽度n 的一张 m * n的乘法表，以及正整数k，你需要返回表中第k 小的数字
1
2
3
4
5
6
7
8
9
输入: m = 3, n = 3, k = 5
输出: 3
解释: 
乘法表:
1	2	3
2	4	6
3	6	9

第5小的数字是 3 (1, 2, 2, 3, 3).
  • 思路：二分查找。令f(x)表示乘法表中小于等于x的数字个数
    • 单调增函数f(x)：sum(min(m, x / i) for i in range(1, n + 1))
    • f(x)=k时，x取值范围[1,k]问题转化为在f(x)中查找第一个大于等于k的x
  • 代码：
1
2
3
4
5
6
7
8
9
10
def findKthNumber(self, m, n, k):
    f = lambda x:sum(min(m, x/i) for i in xrange(1,n+1))
    l,r = 1, k
    while l <= r:
        mid = (l + r) >> 1
        if k <= f(mid):
            r = mid - 1
        else:
            l = mid + 1
    return l
[LeetCode 275] H指数 II
  • 问题：给定一位研究者论文被引用次数的数组（被引用次数是非负整数），数组已经按照升序排列。编写一个方法，计算出研究者的 h 指数。h 指数的定义: “一位有 h 指数的学者，代表他（她）的 N 篇论文中至多有 h 篇论文，分别被引用了至少 h 次，其余的 N - h 篇论文每篇被引用次数不多于 h 次。”
1
2
输入: citations = [0,1,3,5,6]
输出: 3

  • 思路：定义设f(h)表示”h-引用次数第h大的文章的引用次数”，h取值范围为[1,n]，f(h)是非降函数，问题转化为寻找最后一个h使得f(h)<=0，如果没有则返回0

  • 代码：

1
2
3
4
5
6
7
8
9
10
11
def hIndex(self, citations):
    n = len(citations)
    f = lambda i:i-citations[n-i]
    l, r = 1, n
    while l <= r:
        mid = (l+r)>>1
        if f(mid) <= 0:
            l = mid + 1
        else:
            r = mid - 1
    return r
[LeetCode 483] 最小好进制
  • 问题：对于给定的整数 n, 如果n的k（k>=2）进制数的所有数位全为1，则称 k（k>=2）是 n 的一个好进制。以字符串的形式给出 n, 以字符串的形式返回 n 的最小好进制。
  • 思路：
1
2
3
4
1+k+k^2+...k^r=(1-k^(r+1))/(1-k)=n
    1. r有最大值：因为k最小为2，r和k负相关，可以得到r的最大值r<=log(n+1,2)-1
    2. 给定r，k有唯一备选解：又(k+1)^r>k^r+k^(r-1)+...+1 = n >= k^r，得k=int(n^(1./r))
r越大k越小，从大到小遍历r，第一次全1二进制和等于n的返回k
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
def smallestGoodBase(self, n):
    """
    :type n: str
    :rtype: str
    """
    n = int(n)
    max_r = int(math.log(n+1, 2) - 1)
    for r in xrange(max_r,1,-1):
        k = int(n ** (1./r))
        if (k ** (r+1)-1)/(k-1) == n:
            return str(k)
    return str(n - 1)
[LeetCode 878] 第 N 个神奇数字
  • 问题：如果正整数可以被 A 或 B 整除，那么它是神奇的。返回第 N 个神奇数字。由于答案可能非常大，返回它模 10^9 + 7 的结果
1
2
输入：N = 1, A = 2, B = 3
输出：2
  • 思路：
1
2
3
4
二分查找，设f(x)表示<=x的正整数中有多少个神奇数字
    1. f(x) = x/A + x/B - x/lcm(A,B)
    2. x的取值范围为：[1,min(A,B)*N]
    问题转化为，求第一个f(x)=N的x
  • 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def nthMagicalNumber(self, N, A, B):
    """
    :type N: int
    :type A: int
    :type B: int
    :rtype: int
    """
    def gcd(m,n):
        while m:
            m,n = n%m, m
        return n
    def lcm(m,n):
        return m * n / gcd(m,n)
    def f(x):
        return x/A + x/B - x/lcm(A,B)
    
    l,r = min(A,B), min(A,B) * N
    while l <= r:
        mid = (l+r) >> 1
        if N <= f(mid):
            r = mid - 1
        else:
            l = mid + 1
    return l % (10**9 + 7)
[LeetCode 793] 阶乘函数后K个零
  • 问题:f(x) 是 x! 末尾是0的数量。（回想一下 x! = 1 2 3 … x，且0! = 1）找出多少个非负整数x ，有 f(x) = K 的性质。
1
2
3
4
5
6
7
8
9
示例 1:
输入:K = 0
输出:5
解释: 0!, 1!, 2!, 3!, and 4! 均符合 K = 0 的条件。

示例 2:
输入:K = 5
输出:0
解释:没有匹配到这样的 x!，符合K = 5 的条件
  • 思路：
1
2
3
4
n!后缀0的个数K，等于不大于n的所有乘数中，因子5的个数：
    1. f(x)=x/5+x/25+x/125+...+=x/4*(1-(1/5)**n)<x/4，单调增；
    2. f(x) >= x/5;有 5k=>n>4k
    3. 只要存在f(x)==k，那么第一个满足该等式的x必是5的倍数，x+1,x+2,x+3,x+4也都满足有k个0结尾，即只要存在就只有5个，如果不存在有0个；
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def preimageSizeFZF(self, K):
    """
    :type K: int
    :rtype: int
    """
    def count(n):
        res = 0
        while n:
            res += n/5
            n /= 5
        return res
    
    l,r = 4 * K, 5 * K
    while l <= r:
        mid = (l + r) >> 1
        tmp = count(mid)
        if  tmp == K:
            return 5
        elif tmp < K:
            l = mid + 1
        else:
            r = mid - 1
    return 0
[LeetCode 4] 两个排序数组的中位数
  • 问题：给定两个大小为 m 和 n 的有序数组 nums1 和 nums2 。请找出这两个有序数组的中位数。要求算法的时间复杂度为 O(log (m+n)) 。你可以假设 nums1 和 nums2 不同时为空。
1
2
3
4
示例 1:
nums1 = [1, 3]
nums2 = [2]
中位数是 2.0
  • 思路：对齐+二分查找

1
2
3
4
5
6
7
8
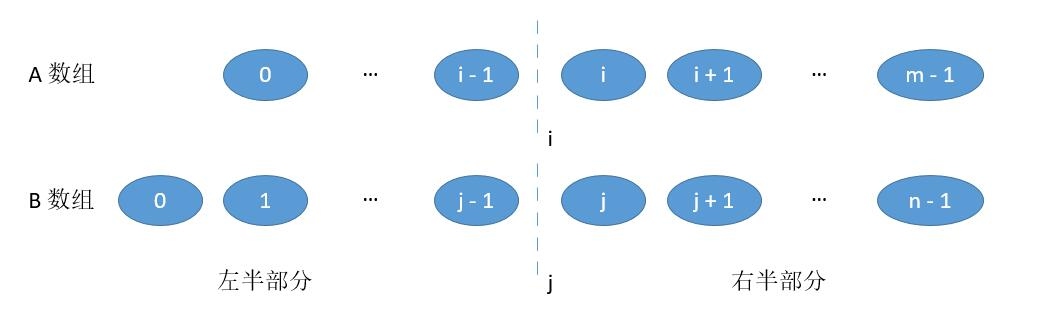
9
将A、B数组(m<=n)在i、j位置对齐，如果对齐位置满足以下两个条件：
    1. i + j = (m+n)/2
    2. 对齐位置左侧(<i,<j)元素总是小于等于右侧元素
注意到，对整个有序数组来说，左侧有(m+n)/2个元素的位置为上中位数，那么：
    1. 如果m+n为奇数，对齐位置右侧元素中的最小元素即为最终的中位数；
    2. 如果m+n为偶数，对齐位置右侧元素中的最小元素为最终的上中位数，左侧最大元素为最终的下中位数；
问题就转化为寻找这样的i,j，如果设f(i)表示左下大于右上个数-左上大于右下个数，那么f(i)是递增函数(非降)，可以通过二分查找在[0,m]范围内找到这样的i：
    1. 如果i < m and A[i] < B[j-1]，在i的右半部分继续查找；
    2. 如果i > 0 and B[j] < A[i-1]，在i的左半部分继续查找；
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def findMedianSortedArrays(self, nums1, nums2):
    A, m, B, n = nums1, len(nums1), nums2, len(nums2)
    if m > n: A, m, B, n = B, n, A, m
    
    l, r = 0, m
    while l <= r:
        i = (l + r) >> 1
        j = (m+n) / 2 - i
        if i > 0 and A[i-1] > B[j]:
            r = i - 1
        elif i < m and B[j-1] > A[i]:
            l = i + 1
        else:
            left_max = max(A[i-1] if i else float('-inf'), B[j-1] if j else float('-inf'))
            right_min = min(A[i] if i < m else float('inf'), B[j] if j < n else float('inf'))
            return right_min if (m+n) & 1 else (left_max + right_min) / 2.
  • 分析：
    • 时间复杂度：我们对较短的数组进行了二分查找，所以时间复杂度是 O（log（min（m，n）））
    • 空间复杂度：只有一些固定的变量，和数组长度无关，所以空间复杂度是 O ( 1 )

树

[LeetCode 230] 二叉搜索树中第K小的元素
  • 问题：如题
  • 思路：统计左子树节点数，如果==k-1则返回根节点，如果>k-1则在左子树中差汇总啊第K小，否则再右子树中查找k-left-1小；
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def kthSmallest(self, root, k):
    """
    :type root: TreeNode
    :type k: int
    :rtype: int
    """
    def getNodes(root):
        return getNodes(root.left) + getNodes(root.right) + 1 if root else 0
    
    if not root:
        return 0
    left = getNodes(root.left)
    if left + 1 == k:
        return root.val
    elif left >= k:
        return self.kthSmallest(root.left, k)
    else:
        return self.kthSmallest(root.right, k-left -1)
[LeetCode 222] 完全二叉树的节点个数
  • 问题：给出一个完全二叉树，求出该树的节点个数
  • 思路：
    1. 如果左右子树高度相同，那么左子树节点数为2^h-1，h为左子树高度，右子树为一个完全二叉树
    2. 如果左右子树高度不同，那么右子树节点数为2^h-1，h为右子树高度，左子树为一个完全二叉树
  • 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def countNodes(self, root):
    """
    :type root: TreeNode
    :rtype: int
    """
    if not root:
        return 0
    l, r = self.get_depth(root.left), self.get_depth(root.right)
    if l == r:
        return 2 ** l + self.countNodes(root.right)
    else:
        return 2 ** r + self.countNodes(root.left)
    
def get_depth(self, root):
    if not root:
        return 0
    return self.get_depth(root.left) + 1

二维矩阵

[LeetCode 74] 二维矩阵中的二分查找
  • 问题：编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：每行中的整数从左到右按升序排列；每行的第一个整数大于前一行的最后一个整数。
1
2
3
4
5
6
7
8
输入:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 3
输出: true
  • 思路：两次二分查找，现在首列进行二分查找，找到则返回，找不到就返回较小的行号，再在所在行进行二分查找，找到就返回，找不到就返回False；
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def searchMatrix(self, matrix, target):
    """
    :type matrix: List[List[int]]
    :type target: int
    :rtype: bool
    """
    def bisect(A, key):
        l,r = 0, len(A) - 1
        while l <= r:
            mid = l + (r-l)/2
            if A[mid] == key:
                return mid
            elif A[mid] < key:
                l = mid + 1
            else:
                r = mid - 1
        return r
    if not any(matrix):
        return False
    tmp = [r[0] for r in matrix]
    x = bisect(tmp, target)
    if x < 0:
        return False
    y = bisect(matrix[x], target)
    return matrix[x][y] == target
[LeetCode 240] 二维矩阵中的二分查找II
  • 问题：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例:

现有矩阵 matrix 如下：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]
给定 target = 5，返回 true。

给定 target = 20，返回 false。
  • 思路：取左下角元素为枢轴值，比它大就把规模缩减到右侧，比它小就把规模缩减到上面。O(m+n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def searchMatrix(self, matrix, target):
    if not matrix:
        return False
    m,n = len(matrix), len(matrix[0])
    r,c = m - 1, 0
    while r >= 0 and c < n:
        mid = matrix[r][c]
        if mid == target:
            return True
        elif mid < target:
            c += 1
        else:
            r -= 1
    return False
[LeetCode 378] 有序矩阵中第K小的元素
  • 问题：给定一个 n x n 矩阵，其中每行和每列元素均按升序排序，找到矩阵中第k小的元素
  • 思路：
1
2
3
4
5
6
思路：二分查找是用于“在递增函数中由y求x的算法”，二分查找用于实际问题的精髓在于将原始问题转化为这在递增函数中由y求x的问题，然后定义递增函数的三要素：定义域、值域、映射；具体的，需要定义函数f(x)，定义域[l,r]，目标值target
    在本问题中，寻找第k小的数，f(x)=k，
        1. 定义域：所有可能的数作为下标，范围为左上角到右下角的整数
        2. 值域：第几小作为y
        3. 映射：计算x是第几小，可以通过在每行进行二分查找求和得到
    因为f(x)存在重复元素，应返回第一个数
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def kthSmallest(self, matrix, k):
    """
    :type matrix: List[List[int]]
    :type k: int
    :rtype: int
    """    
    l, r = matrix[0][0], matrix[-1][-1]
    while l <= r:
        mid = (l+r) >> 1
        loc = sum(bisect.bisect(m, mid) for m in matrix)
        if loc >= k:
            r = mid - 1
        else:
            l = mid + 1
    return l

旋转数组

[LeetCode 153]查找旋转数组中的最小值
  • 问题：假设按照升序排序的数组在预先未知的某个点上进行了旋转，假设不含重复元素，请找出其中最小的元素。
1
2
输入: [3,4,5,1,2]
输出: 1
  • 思路：中值和右边界比较，l==r时退出循环；如果中间的值大于右侧的值，说明最小值肯定在mid右侧，否则最小值肯定在mid或mid左侧。
  • 代码：
1
2
3
4
5
6
7
8
9
def findMin(self, nums):
    l, r = 0, len(nums) - 1
    while l != r:
        mid = (l+r) >> 1
        if nums[mid] > nums[r]:
            l = mid + 1
        else:
            r = mid
    return nums[l]
  • 分析：时间复杂度为O(lgn)
[LeetCode 154]查找含重复元素的旋转数组中的最小值
  • 问题：同153，但是数组中可能含有重复元素
  • 思路：中值与右边界比较，l==r时退出循环(l<r时mid<r)；如果中值大于右边界，说明最小值在mid右侧，如果中值小于右边界说明最小值在mid或mid左侧，如果中值等于右边界说明最小值在r左侧；
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
def findMin(self, nums):
    l,r = 0, len(nums)-1
    while l != r:
        mid = (l+r) >> 1
        if nums[mid] > nums[r]:
            l = mid + 1
        elif nums[mid] < nums[r]:
            r = mid
        else:
            r -= 1
    return nums[l]
  • 分析：最坏时间复杂度为O(n)，平均O(lgn)

动态规划

[LeetCode 887] 鸡蛋掉落
  • 问题:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N  共有 N 层楼的建筑。

每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。

你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。

每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。

你的目标是确切地知道 F 的值是多少。

无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？

输入：K = 1, N = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，我们肯定知道 F = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，我们肯定知道 F = 1 。
如果它没碎，那么我们肯定知道 F = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 F 是多少
  • 思路：
1
2
3
4
5
6
7
理解题意：用[0,0,...,1,1,1]表示每层楼的结果，0表示不碎，1表示碎，任务是在与1的比较次数<=K的前提下，最少比较几次才能找到最后一个0的位置。
    思路：动态规划，用dp[m][k]表示使用k个鸡蛋移动m次所能检验的最大层数
        1. dp[m][k] = dp[m-1][k-1] + dp[m-1][k] + 1，蛋碎+蛋不碎+1
        2. 边界：dp[m][0]=0,dp[0][k]=0
        问题转化为求最小的m使得dp[m][K]>=N, 令f(m)=dp[m][K]，f(m)单调增，求第一个大于等于N的m（bisect_left），二分查找
        1. f(m)=dp[m][K]
        2. m 取值范围为 [1,N]
  • 代码:
1
2
3
4
5
6
7
8
9
10
11
def superEggDrop(self, K, N):
    """
    :type K: int
    :type N: int
    :rtype: int
    """
    dp = [[0] * (K + 1) for i in range(N + 1)]
    for m in range(1, N + 1):
        for k in range(1, K + 1):
            dp[m][k] = dp[m - 1][k - 1] + dp[m - 1][k] + 1
        if dp[m][K] >= N: return m
[LeetCode 354] 俄罗斯套娃信封问题
  • 问题:给定一些标记了宽度和高度的信封，宽度和高度以整数对形式 (w, h) 出现。当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。
1
2
3
输入: envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出: 3 
解释: 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
  • 思路：
1
2
3
排序后变成求最长递增子序列问题
    1. 排序：首先按照宽度排序，宽度相同则高度小的在前面；这一点至关重要，可防止宽度相同时，大的包裹小的
    2. 最长递增子序列：维护一个辅助数组，每个元素的下标代表以该元素结尾的最长递增子序列的长度-1
  • 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def maxEnvelopes(self, envelopes):
    """
    :type envelopes: List[List[int]]
    :rtype: int
    """
    envelopes.sort(key=lambda x:(x[0],-x[1]))
    
    dp = []
    count = 0
    for _, h in envelopes:
        idx = bisect.bisect_left(dp, h)
        if idx > len(dp) - 1:
            dp.append(h)
        else:
            dp[idx] = h
    return len(dp)
[LeetCode 410] 分割数组的最大值
  • 问题:给定一个非负整数数组和一个整数 m，你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。
1
2
3
4
5
6
7
8
9
10
11
输入:
nums = [7,2,5,10,8]
m = 2

输出:
18

解释:
一共有四种方法将nums分割为2个子数组。
其中最好的方式是将其分为[7,2,5] 和 [10,8]，
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。
  • 思路:
1
2
3
4
5
6
7
思路1：动态规划，超时。令dp[i][m]表示以i为结尾(不含i)，分为m段，各段最大值的最小值；有：
        1. dp[i][m] = min(max(dp[j][m-1], sum(nums[j:i]))),j=1,2,...,i-1
        2. 边界：i < m时，取无穷，i==m时，取所有元素的最大值
    思路2：二分查找。设f(x)表示使得子数组各自和的最大值的最小值为x时，所需的最小子数组数是否<=m，则：
        1. x取值范围为[sum(nums)/m,sum(nums)]
        2. f(x)取值[0,0,...,1,1]
        问题转化为求f(x)第一次取1时的x
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def splitArray(self, nums, m):
    """
    :type nums: List[int]
    :type m: int
    :rtype: int
    """
    def valid(x):
        count = 1
        cur = 0
        for num in nums:
            cur += num
            if cur > x:
                count += 1
                if count > m:
                    return False
                cur = num
        return True
    
    l,r = max(nums), sum(nums)
    while l <= r:
        mid = (l+r) >> 1
        if valid(mid):
            r = mid - 1
        else:
            l = mid + 1
    return l
[LeetCode 719] 找出第 k 小的距离对(至尊二分查找)
  • 问题：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

给定一个整数数组，返回所有数对之间的第 k 个最小距离。一对 (A, B) 的距离被定义为 A 和 B 之间的绝对差值。

示例 1:

输入：
nums = [1,3,1]
k = 1
输出：0 
解释：
所有数对如下：
(1,3) -> 2
(1,1) -> 0
(3,1) -> 2
因此第 1 个最小距离的数对是 (1,1)，它们之间的距离为 0。

  • 思路：二分查找+含重复元素的二分查找。令f(x)表示距离小于等于x的数对个数，观察到f(x)是单调增(含重复元素)的函数，寻找数对之间第k小的距离，即是寻找x使得f(x-1)<k<=f(x)，这样的问题可以通过二分查找求解；计算f(x)时可以先对nums进行排序，f(x)=sum(i - bisect.bisect_left(nums, num - mid, 0, i) for i, num in enumerate(nums))

  • 代码：

1
2
3
4
5
6
7
8
9
10
11
def smallestDistancePair(self, nums, k):
    nums.sort()
    l, r = 0, nums[-1] - nums[0]
    while l <= r:
        mid = (l+r) >> 1
        cur = sum(i - bisect.bisect_left(nums, num - mid, 0, i) for i, num in enumerate(nums)) 
        if k <= cur:
            r = mid - 1
        else:
            l = mid + 1
    return l

其他二分查找问题

[LeetCode 852] 山脉数组的峰顶索引
  • 问题：
1
2
3
4
5
我们把符合下列属性的数组 A 称作山脉：

A.length >= 3
存在 0 < i < A.length - 1 使得A[0] < A[1] < ... A[i-1] < A[i] > A[i+1] > ... > A[A.length - 1]
给定一个确定为山脉的数组，返回任何满足 A[0] < A[1] < ... A[i-1] < A[i] > A[i+1] > ... > A[A.length - 1] 的 i 的值。
  • 思路：如果A[mid] < A[mid+1]，说明山峰在mid右侧，否则说明山峰在mid或mid左侧；
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
def peakIndexInMountainArray(self, A):
    """
    :type A: List[int]
    :rtype: int
    """
    l, r = 0, len(A)-1
    while l != r:
        mid = (l + r) >> 1
        if A[mid] < A[mid+1]:
            l = mid + 1
        else:
            r = mid
    return l
[LeetCode 875] 爱吃香蕉的珂珂
  • 问题：
1
2
3
4
5
6
7
珂珂喜欢吃香蕉。这里有 N 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 H 小时后回来。

珂珂可以决定她吃香蕉的速度 K （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 K 根。如果这堆香蕉少于 K 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。  

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 H 小时内吃掉所有香蕉的最小速度 K（K 为整数）
  • 思路：
1
2
3
4
1. f(x)表示速度为x时需要多少个小时吃完，f(x)
=sum(math.ceil(p*1./k) for p in piles)，为单调减函数
2. x取值范围：l,r = 1, max(piles)
3. 问题转化:求f(x)<=H的最小x
  • 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def minEatingSpeed(self, piles, H):
    """
    :type piles: List[int]
    :type H: int
    :rtype: int
    """
    def helper(k):
        return sum(math.ceil(p*1./k) for p in piles)
    
    l,r = 1, max(piles)
    while l <= r:
        mid = (l+r) >> 1
        if helper(mid) <= H:
            r = mid - 1
        else:
            l = mid + 1
    return l

[360 笔试]
  • 问题：

  • 思路：
1
2
3
思路1: 直接对a[l-1:r]进行集合运算，返回长度，时间O(qn)，空间O(n)；超时
思路2：存储count[n][m]，表示<=n时每种花的数目，时间O(mq)，空间O(mn)；超内存
思路3：二分查找，存储每种花出现的下标列表，给定[l,r]，每次在每种花中进行二分查找，对l返回第一个大于等于l的下标x，对r返回第一个大于r的下标y，如果y>l则说明该花在[l,r]内；
  • 代码：
n,m = map(int, raw_input().split())
a = map(int, raw_input().split())
q = input()

d = collections.defaultdict(list)
for i,x in enumerate(a):
    d[x].append(i)

def solve(l,r):
    l,r = l-1, r-1
    res = 0
    for key in d:
        x = bisect.bisect_left(d[key], l)
        y = bisect.bisect_right(d[key], r)
        res += (y > x)
    return res

for _ in xrange(q):
    l,r = map(int, raw_input().split())
    print solve(l,r)
坚持原创技术分享，您的支持将鼓励我继续创作！