机器学习：基础算法（四）—— NB

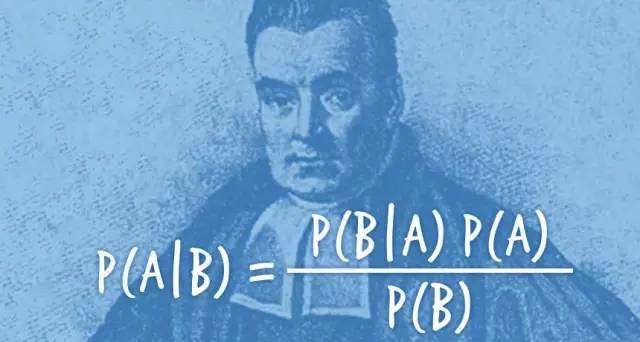
朴素贝叶斯（naive Bayes，NB）是基于贝叶斯定理与特征条件独立性假设的分类方法。其模型是通过学习先验概率和类条件概率来得到后验概率的生成式模型。其策略为后验概率最大，等价于0-1损失下的期望风险最小化策略。其算法为通过极大似然估计来求解各项概率。

模型

贝叶斯通过训练数据学习联合概率分布$p(x,y)$，具体地：

$$\begin{align*} &p(Y=c_k),\ \ k=1,2...,K\\ &p(X=x|Y=c_k)=p(X^1=x^1,X^2=x^2,...,X^D=x^D|Y=c_k),\ \ k=1,2,...,K \end{align*}$$

后者有指数级的参数，其估计实际是不可行的，NB对类条件概率做出了条件独立性假设，将参数个数降到线性的，朴素因此得名：

$$p(X=x|Y=c_k)=\prod_{d=1}^{D}p(X^d=x^d|Y=c_k)$$

由贝叶斯定理和全概率公式我们可以得到贝叶斯公式：

$$\begin{align*} p(Y=c_k|X=x) &= \frac{p(Y=c_k)p(X=x|Y=c_k)}{p(X=x)}\\ &=\frac{p(Y=c_k)\prod_{d=1}^{D}p(X^d=x^d|Y=c_k)}{\sum_{k=1}^{K}p(Y=c_k)\prod_{d=1}^{D}p(X^d=x^d|Y=c_k)} \end{align*}$$

对不同的分类，分母都相同，因此贝叶斯模型可表示为：

$$y = arg \ \underset{c_k}{max} \ p(y=c_k)\prod_{d=1}^{D}p(X^d=x^d|Y=c_k)$$

策略

后验概率最大（MAP）等价于0-1损失下的期望风险最小化的策略：

$$\begin{align*} R_{exp}(f)&=E[L(y,f(x))]\\ &=E_X \sum_{k=1}^{K}L(c_k,f(X))p(c_k|X)\\ \end{align*}$$

为了极小化期望风险，可以对每一个$X=x$进行极小化：

$$\begin{align*} f(x)&=arg\ \underset{c_k}{min}\ \sum_{k=1}^{K}L(c_k,f(X=x))p(c_k|X=x)\\ &=arg\ \underset{c_k}{min}\ \sum_{k=1}^{K}(p(y\neq c_k|X=x))\\ &=arg\ \underset{c_k}{min}\ \sum_{k=1}^{K}(1-p(y=c_k|X=x))\\ &=arg\ \underset{c_k}{max}\ p(y=c_k|X=x) \end{align*}$$

算法

不同的朴素贝叶斯方法的区别仅在于对特征的类条件概率分布 $P(x_i \mid y)$ 的假设不同，它们都是用极大似然的方法来估计分布参数。

高斯朴素贝叶斯（Gaussian Naive Bayes）

高斯朴素贝叶假设所有特征的类条件概率服从高斯分布（当特征为连续时一般选用高斯贝叶）；

$$P(x^d \mid y) = \frac{1}{\sqrt{2\pi\sigma^2_y}} \exp\left(-\frac{(x^d - \mu_y)^2}{2\sigma^2_y}\right)$$

采用极大似然法估计 $\sigma_y$ 和 $\mu_y$。

多项式朴素贝叶斯（Multinomial Naive Bayes）：

多项式朴素贝叶斯假设所有特征的类条件概率服从多项式分布，在类别为$ck$条件下，特征$X^d$的概率分布可以用一个参数向量$\theta^d_k = (\theta^d{k1},\ldots,\theta^d_{kn}) $来表示(当特征为多类别离散变量时选用多项式NB)；

可以用极大似然法来估计相应的概率：

$$\begin{align*} &p(Y=c_k)=\frac{N_k}{N}\\ &\theta^d_{kx^d} = p(X^d=x^d|Y=c_k)=\frac{N_{k,x^d}}{N_k} \end{align*}$$

• $N_k$：所有样本中类别为$c_k$的个数；
• $N_{k,x^d}$：类别为$c_k$且第d维为$x^d$的样本个数；

平滑版极大似然：极大似然估计可能会出现估计的概率为0的情况，影响侯艳艳概率的计算，使分类出现偏差，可以用平滑方法解决这一问题，具体的就是在计算每个概率时，我们在分母的范围内为分子的每种可能结果加$\lambda$：

$$\begin{align*} &p(Y=c_k)=\frac{N_k+\lambda}{N+K\lambda}\\ &p(X^d=x^d|Y=c_k)=\frac{N_{k,x^d}+\lambda}{N_k + s_d\lambda} \end{align*}$$

• K：y类别个数；
• $s_d$：数据集中当类别为$c_k$时，第i维坐标可能取值个数；
• $\lambda$: 取1时叫拉普拉斯平滑

伯努利朴素贝叶斯（ Bernoulli Naive Bayes）

伯努利朴素贝叶斯假设特征的类条件分布为伯努利分布（当特征为二值特征时使用）：

$$\begin{align*} &p(X^d=x^d \mid Y=c_k) = p \\ &p(X^d\neq x^d \mid Y=c_k) = 1-p \end{align*}$$

通过极大似然估计p。

实例

比较朴素贝叶斯与SVM的学习曲线：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import cross_validation
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.learning_curve import learning_curve


def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
                        n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
    plt.figure()
    plt.title(title)
    if ylim is not None:
        plt.ylim(*ylim)
    plt.xlabel("Training examples")
    plt.ylabel("Score")
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    plt.grid()

    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
                     train_scores_mean + train_scores_std, alpha=0.1,
                     color="r")
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
                     test_scores_mean + test_scores_std, alpha=0.1, color="g")
    plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
             label="Training score")
    plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
             label="Cross-validation score")

    plt.legend(loc="best")
    return plt


digits = load_digits()
X, y = digits.data, digits.target


title = "Learning Curves (Naive Bayes)"
# Cross validation with 100 iterations to get smoother mean test and train
# score curves, each time with 20% data randomly selected as a validation set.
cv = cross_validation.ShuffleSplit(digits.data.shape[0], n_iter=100,
                                   test_size=0.2, random_state=0)

estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01), cv=cv, n_jobs=4)

title = "Learning Curves (SVM, RBF kernel, $\gamma=0.001$)"
# SVC is more expensive so we do a lower number of CV iterations:
cv = cross_validation.ShuffleSplit(digits.data.shape[0], n_iter=10,
                                   test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv, n_jobs=4)

plt.show()

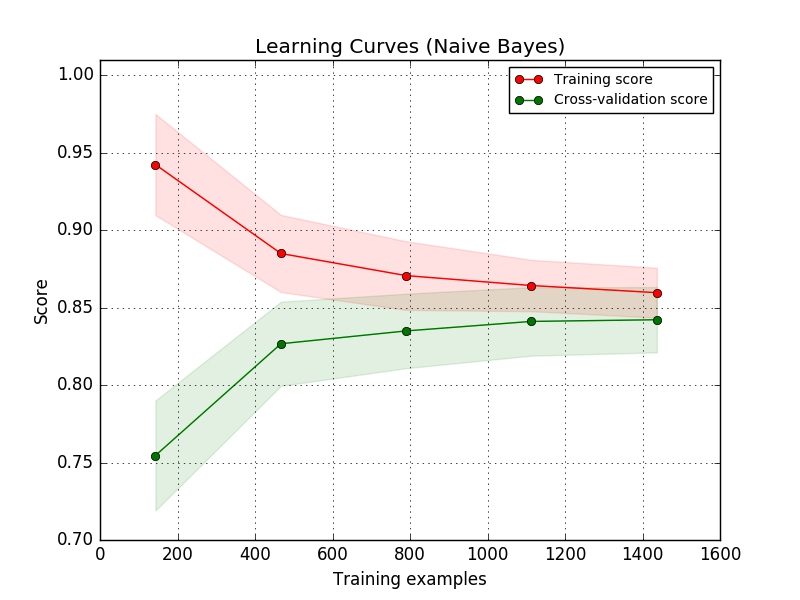
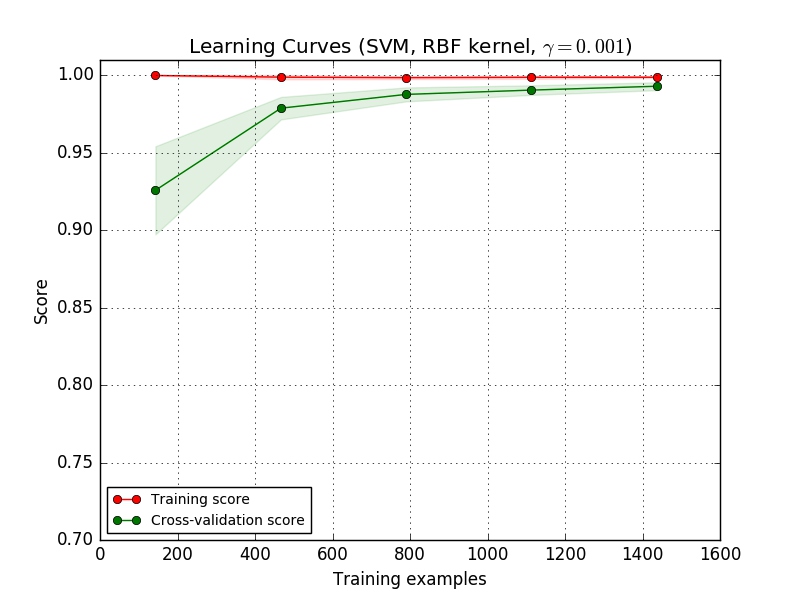
• 对于SVM（复杂模型）：当数据量小的时候，训练误差为0，但是测试误差较大；随着训练数据增加，训练误差缓慢增加，验证误差逐渐下降；当数据量足够大的时候，训练误差和测试误差维持在一个较低水平；
• 对于朴素贝叶斯（简单模型）：当数据量小的时候，训练误差相对复杂模型更大，验证误差也比较大；随着数据量增加，训练误差迅速增加，验证误差不断下降；当数据量足够大的时候，训练误差和测试误差维持在一个较高水平；

评价

• 优点：
  1. 实现简单
  2. 对缺失数据不敏感
  3. 适合增量学习
• 缺点：
  1. 朴素贝叶斯建立在独立性假设的基础上，当特征间相关性较大时，模型效果不好；
  2. 不好的先验假设会影响模型性能
  3. 对输入数据的表达形式比较敏感