机器学习：优化算法（二）——（拟）牛顿法

牛顿法(Newton method)和拟牛顿法(quasi Newton method)也是求解最优化问题的常用迭代方法。当目标函数是凸函数时，可以得到全局最优解，否则不能保证得到全局最优解，但是其收敛速度相比梯度下降法要快。

假设 $f(x)$ 具有二阶连续偏导，考虑无约束最优化问题：

$$x^*=\underset{x \in \mathbb{R}^n}{min}\ f(x)$$

牛顿法

牛顿法原理

将$f(x)$在$x_k$附近进行二阶泰勒展开：

$$f(x)=f(x_k)+g_k^T(x-x_k)+\frac{1}{2}(x-x_k)^TH(x_k)(x-x_k)$$

• $g(x)$：$f(x)$在x处的一阶偏导
• $H(x)$：$f(x)$在x处的二阶偏导矩阵(海赛矩阵)

两边同时取导，得到过点$(x_k,g_k)$的切线方程：

$$g=g_k+H_k(x-x_k)$$

$f(x)$ 取极值的必要条件是在极值处偏数为0，即求$g(x)=0$，该问题可以用牛顿法求解：

1、选取合适的初值$x_0$，置k=0
2、计算$g_k$，若$\left | g_k \right | < \varepsilon $，则停止计算，得到$x^=x_k$，否则用$g(x)$在当前位置的切线与x轴的交点*更新$x_k$（因此，牛顿法也被称为“切线法”）

$$x_{k+1}=x_k-H_k^{-1}g_k$$

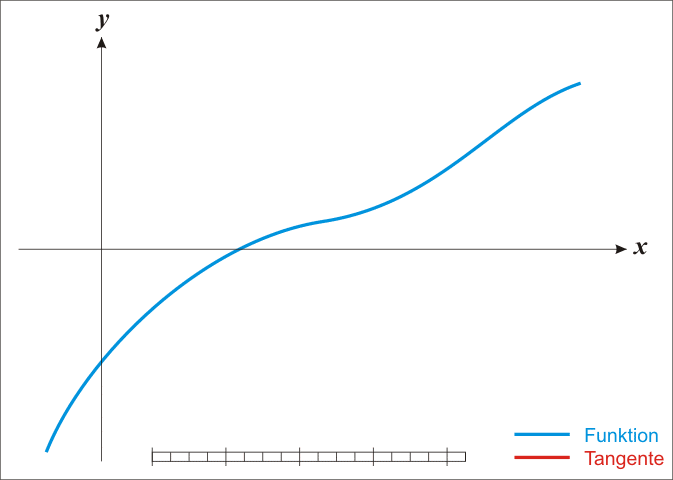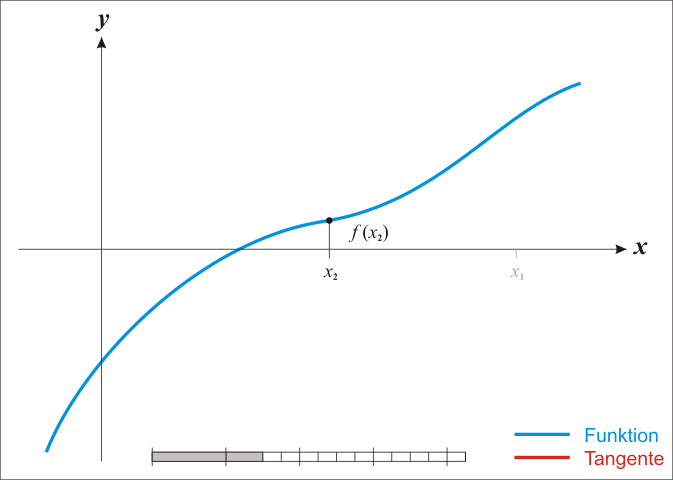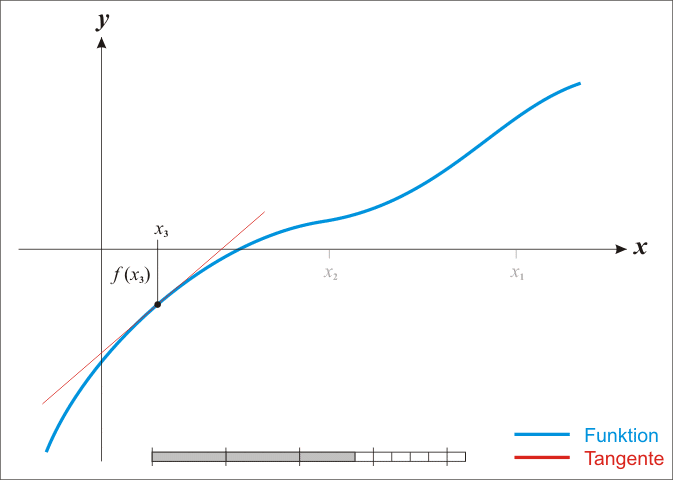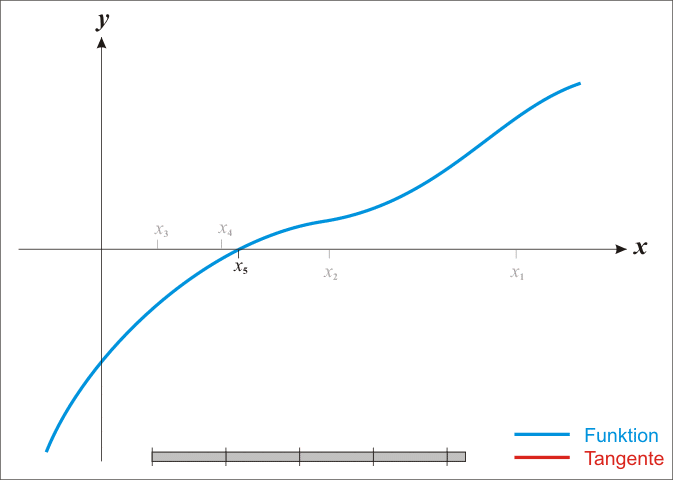
牛顿法有效性证明

因为 $f(x)$ 是凸函数，那么$H_k$为正定矩阵($H_k^{-1}$也是正定矩阵)，即：

$$H_k^{-1}g_k=\lambda g_k,\ \lambda > 0$$

可以保证x更新方向总是沿着$f(x)$的负梯度方向：

$$x_{k+1}=x_k-H_k^{-1}g_k=x_k-\lambda g_k$$

牛顿法优缺点

优点：

1. 更快：相比一阶收敛的梯度下降法，牛顿法二阶收敛，收敛速度更快，牛顿法不但考虑了搜索的方向，还用二阶逼近来估计步长
2. 更准：从几何上看，牛顿法是用一个二次曲面来拟合当前位置的局部曲面，而梯度下降则是用一个平面拟合当前局部曲面，所以牛顿法选择的下降路径会更符合真实的最优下降路径

缺点:

1. 牛顿法仍然是一种局部最优化算法，在非凸问题中一般无法取到全局最优解；
2. 每次迭代需要求解目标函数的海赛矩阵的逆矩阵，计算复杂度高；

拟牛顿法

拟牛顿法对牛顿法改进的基本思路是：使用某个矩阵作为海赛矩阵或海赛矩阵的逆矩阵的近似，从而避免求解海赛矩阵。

拟牛顿条件：在切线方程中取$x=x_{k+1}$

$$g_{k+1}-g_k=H_k(x_{k+1}-x_{k})$$

记$yk=g{k+1}-gk,\ \delta_k=x{k+1}-x_k$，则：

$$y_k=H_k\delta_k$$

DFP(Davidon-Fletcher-Powell)算法

DFP使用$G_k$作为$H_k^{-1}$的近似，在每次迭代时通过如下公式更新$G_k$：

$$G_{k+1}=G_{k}+P_k+Q_k$$ $$G_{k+1}y_k=G_{k}y_k+P_ky_k+Q_ky_k$$

为使$G_{k+1}$满足拟牛顿条件，可使：

$$p_ky_k=\delta_k$$ $$G_{k}y_k=-Q_ky_k$$

容易找到这样的$P_k,\ Q_k$，得到：

$$G_{k+1}=G_k+\frac{\delta_k \delta_k^T}{ \delta_k^T\delta_k}-\frac{G_ky_ky_k^TG_k}{y_k^TG_ky_k}$$

可以证明，如果初始矩阵$G_0$是正定的，则迭代过程中的每个矩阵$G_k$都是正定的。

1、选取初始点$x_0$，取$G_0$为正定对称矩阵
2、计算$g_k$，若$\left | g_k \right | < \varepsilon $，则停止计算，得到$x^*=x_k$，否则:
（1）计算$p_k=-G_kg_k$
（2）一维搜索$\lambda_k$，满足：

$$f(x_k+\lambda_kp_k)=\underset{\lambda\geqslant 0}{min}f(x_k+\lambda p_k)$$

（3）置$x{k+1}=x_k+\lambda p_k$
（4）计算$g{k+1}$，更新$G_{k+1}$

BFGS(Davidon-Fletcher-Powell)算法

BFGS用$B_k$作为$H_k$的近似，在每次迭代时通过如下公式更新$B_k$：

$$B_{k+1}=B_{k}+P_k+Q_k$$ $$B_{k+1}\delta_k=B_{k}\delta_k+P_k\delta_k+Q_k\delta_k$$

为使$G_{k+1}$满足拟牛顿条件，可使：

$$p_k\delta_k=y_k$$ $$B_{k}\delta_k=-Q_k\delta_k$$

容易找到这样的$P_k,\ Q_k$，得到：

$$B_{k+1}=B_k+\frac{y_k y_k^T}{ y_k^T\delta_k}-\frac{B_k\delta_k\delta_k^TB_k}{\delta_k^TB_k\delta_k}$$

可以证明，如果初始矩阵$B_0$是正定的，则迭代过程中的每个矩阵$B_k$都是正定的。

1、选取初始点 $x_0$，取 $B_0$ 为正定对称矩阵
2、计算$g_k$，若$\left | g_k \right | < \varepsilon $，则停止计算，得到$x^*=x_k$，否则:

（1）由$B_kp_k=-g_k$计算$p_k$
（2）一维搜索$\lambda_k$，满足：

$$f(x_k+\lambda_kp_k)=\underset{\lambda\geqslant 0}{min}f(x_k+\lambda p_k)$$

（3）置$x{k+1}=x_k+\lambda p_k$
（4）计算$g{k+1}$，更新$B_{k+1}$

对比梯度下降和牛顿法

	更新公式	优点	缺点
梯度下降	$x_{k+1}=x_k-\eta \nabla_xf(x)$	简单	局部最优、速度慢
牛顿法	$x_{k+1}=x_k-H_k^{-1}g_k$	更快更准	局部最优、复杂度高
BFP	$x_{k+1}=x_k-G_kg_k$	不用计算海赛矩阵
BFGS	$x_{k+1}=x_k-B_kg_k$	不用计算海赛矩阵