数据科学：因果推断（二）—— Rubin 因果模型（RCM）

鲁宾因果模型（Rubin causal model, RCM），也称内曼-鲁宾因果模型（Neyman–Rubin causal model），是一种基于潜在结果框架（framework of potential outcomes）的因果推断方法，以杰西·内曼（Jerzy Neyman）和唐纳德·鲁宾（Donald Rubin）的名字命名。潜在结果的概念最早是由 Neyman（1923）在研究重复随机化农业实验中提出的，由于该文用波兰语写成，当时没有引起学界的关注。Rubin（1974）重新独立地提出了潜在结果的概念，并将它的使用推广到观测研究领域，从而形成了目前的潜在结果框架。RCM 有三个基本要素：潜在结果、稳定性假设、分配机制。

潜在结果

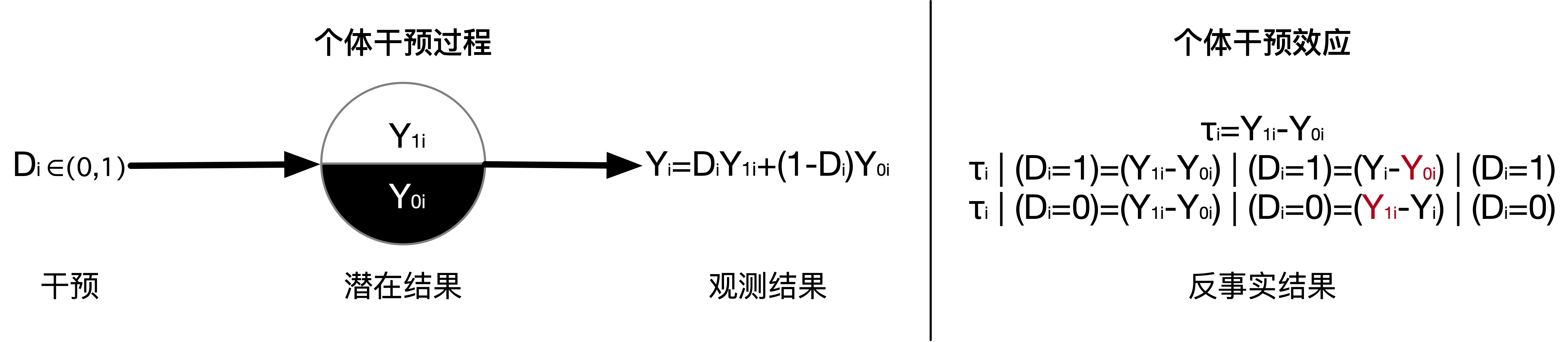
干预

在因果推断中，必须有干预（Intervention），没有干预就没有因果（Rubin，1974）。干预可以是一项政策、一项措施或一项活动等，比如实施 4 万亿财政刺激方案，服用某种新药等。本文主要讨论二值干预变量，两个值分别对应于积极的行动和被动的行动，分别称为干预和控制，受到对应干预的个体分别称为干预组和控制组。

干预和控制只是干预变量的两种状态的标签，具体哪个状态被称为干预，哪个状态称为控制并不重要，两种状态实际上是对称的，可以互换，取决于研究者的目的和偏好。比如，对于药物试验来说，干预是服用药物，控制是不服用药物。

潜在结果

在干预状态实现之前，有几个干预状态就有几个潜在结果（Potential outcome），而干预状态实现之后，只有一个潜在结果是可以观测到的。可以将潜在结果看作常数，对于每个特定的个体，他在两种干预状态下的潜在结果是给定的，不依赖于最终实现的干预状态，这一点对于理解 Rubin 因果模型很关键。

比如，考察大学教育对个人收入的影响，干预变量或原因变量是大学教育，那么对于任意个体 $i$ 有两种干预状态，用 $Di$ 来表示，$D_i=1$ 表示个体 $i$ 完成了大学教育，$D_i=0$ 表示个体 $i$ 完成高中教育。无论个体实际是完成大学教育还是高中教育，事前每个个体均有两种可能的状态：完成高中教育或完成大学教育。每一个状态下对应于一个潜在结果，$Y{1i}$ 表示个体 $i$ 在状态$Di=1$ 下的潜在结果，$Y{0i}$ 表示个体 $i$ 在状态 $Di=0$ 下的潜在结果。对个体而言，这两个潜在结果可以看作是确定性的变量，不因个体干预变量的实现状态而改变。比如个体 $i$ 完成大学教育状态下的收入为 $8000$ 元，即 $Y{1i}=8000$，仅完成高中教育状态下收入为 6000 元，即 $Y_{0i}=6000$。如果个体 $i$ 最后实际完成了大学教育，那么其两种干预状态下的潜在结果仍然是（8000，6000），如果个体 $i$ 最后实际完成的是高中教育，其两种干预状态下的潜在结果还是（8000，6000），不因个体最后实现的状态而改变。

观测结果 VS 反事实结果

当干预状态实现之后，我们仅能观测到实现状态下的潜在结果，称为观测结果（Observation outcome），没有实现状态下的潜在结果是无法观测的，通常称为反事实结果（Counterfactual outcome）。比如个体 $i$ 最终完成了大学教育，那么观测到的干预状态是 $Di=1$，我们可以观测到潜在结果 $Y{1i}$，即个体 $i$ 完成大学教育后的收入。他完成了大学教育，我们就不能观测到他没有完成大学教育时的潜在结果 $Y_{0i}$，即仅完成高中教育时的收入。一个人不可能同时踏入两条河流，不可能同时处于两种状态，因而，观测研究中，不可能同时看到个体所有的潜在结果。无法同时观测到个体所有潜在结果的现象称为因果推断的基本问题（Holland，1986）。

观测结果 $Y_i$ 与潜在结果之间的关系，可以用下面的公式表示：

$$\begin{align*} Y_i&=D_iY_{1i}+(1-D_i)Y_{0i}\\ &=\left\{\begin{matrix} Y_{1i}, & \text{如果}\ D_i = 1 \\ Y_{0i}, & \text{如果}\ D_i = 0 \end{matrix}\right. \end{align*} \tag {1}$$

潜在结果和观测结果的区分是现代统计学和现代计量经济学的重要标志，是经济学经验研究“可信性革命”的关键，也是区分描述性研究（descriptive study）和因果研究（causal study）的标志。

干预效应/因果效应

有了潜在结果的概念，个体因果效应的定义非常直观，不需要对分配机制进行任何内生性或外生性的假设，也不需要对结果变量的函数形式进行任何假设，对于个体 $i$，某项干预的因果效应是两种状态下的潜在结果的比较：

$$\tau_i=Y_{1i}-Y_{0i} \tag {2}$$

关于因果效应的定义有两点说明：

1. 因果效应仅依赖于潜在结果，与观测结果无关：回到大学教育如何影响收入的例子，无论个体 $i$ 是否完成了大学教育，大学教育对其个人的因果影响都取决于其两种状态下的潜在结果，并且是固定不变的，不依赖于个体最终实现的干预状态；如果个体 $i$ 完成了大学教育，大学教育对其收入的影响是每个月收入增加 2000 元；如果个体 $i$ 仅完成高中教育，那么，如果他能完成大学教育，则其收入的影响也是每月增加 2000 元。
2. 因果效应是干预后同一时间、同一物理个体潜在结果的比较：比如考察某种药物对感冒的治疗效果，干预状态是吃药或不吃药，对应的潜在结果是治愈感冒或没有治愈；因果效应应该定义为我现在吃药和不吃药对应潜在结果的比较，而不能用我现在吃药和昨天我没有吃药时的潜在结果比较；因为昨天的我和今天的我不是同一个我，我今天不吃药的潜在结果和昨天不吃药的潜在结果可能是不一样的，所以在评价今天我吃药的因果效应时，应该是今天我吃药和今天我不吃药时潜在结果的比较。

反事实结果估计

因果效应的定义仅依赖于不同潜在结果的比较，对于给定个体，研究者只能观察到该个体一个状态下的潜在结果，因而，如果仅有一个个体，我们是没有办法得到个体因果效应的。因果推断的核心内容，实际上是想办法将未观测到的潜在结果估计出来，即反事实结果估计。估计反事实结果必须要用到多个个体，多个个体的选择方式有两种：

1. 同一个体的不同时间：比如，判断一种药物是否对感冒有治疗效果，我们往往根据自己以往的经历。我以前感冒的时候吃药感冒就好了，我今天没吃药，头就很痛，因而，我们认为药物有治疗效果。其实这种推断中，我们进行了很强的假设，我们假设过去的经验可以作为今天吃药的反事实结果。如果这一假设不成立，我们就不能用过去吃药的结果作为今天吃药的反事实结果。因为今天的“我”与过去的“我”是不同的个体，我今天可能心情不好，不吃药头很痛，即使吃药，头仍然是痛的。这并不一定说明药没有治疗效果，而是因为我心情沮丧，使我的头更痛了，即我的头痛还混杂了其他的影响因素。
2. 同一时间的不同个体：很多时候，我们的推断是利用同一时间不同个体的信息来估计反事实结果。比如考虑大学教育对收入的影响。在上大学之前，我们不确定大学能给我们带来什么。我们只知道目前我的结果是什么样子，或收入是什么水平。但不知道大学毕业之后收入会是什么水平。那我们在决定是否上大学时，是怎么作出决定的呢？我们可能会观察那些上了大学的人，可能是亲戚或朋友家的孩子，现在已经大学毕业了，有个很好的工作，获得比较满意的收入。那我们在作决策时是怎么做的呢？我们可能将他们的结果或收入作为我们上大学的潜在收入，从而决定是否上大学。

稳定性假设

RCM 的第二个要素是稳定个体干预值假（Stable Unit Treatment Value Assumption, SUTVA），简称稳定性假设（Rubin，1980），SUTVA 有两层含义：

1. 不同个体的潜在结果之间不会交互影响：比如，我们住在同一间宿舍，我们两个都感冒了，如果药物对我头痛的治疗效果依赖于你有没有吃药，那就不满足稳定性假设；在社会科学中，没有交互影响的假设可能不成立，社会科学的研究对象往往是人的行为，个人行为之间往往存在交互影响；但是，在不存在交互影响的假设下，因果推断更加容易，通常假设不同个体之间不存在交互影响。
2. 干预水平对所有个体都是相同的：比如考察药物的治疗效果，那么给所有病人的药物在药效上都应该是一样的，不能有的人有效成分是全额的，有的人是半额的；实际研究中，往往很难完全满足这一要求，通常会忽略掉这种差异，更加关注稳定性假设的第一项要求。

分配机制

分配机制是描述为什么有的人在干预组，有的人在控制组的机制。分配机制决定了个体哪个潜在结果会被实现，可以被观测到。在因果推断中，分配机制非常重要，来看一个“手术相对于药物的治疗效果”的例子：

在潜在结果列可以看出，对于病人 1 和病人 3 来说，手术治疗效果优于药物治疗，而对于病人 2 和病人 4 来说，药物治疗优于手术治疗。假设现实中医生具有很好的医术或鉴别力，可以让病人选择对他最有利的治疗方案，从而实现的分配机制如表中第 5 列所示，让 1 和 3 号病人接受手术治疗，让 2 和 4 号病人接受药物治疗，最终我们可以观测到 1、3 病人的 $Y{1i}$ 以及 2、4 病人的 $Y{0i}$，如观测结果列所示。如果不清楚分配机制，直接用两组观测结果进行比较，将会发现手术治疗平均寿命为 6 年，而药物治疗平均寿命为 7 年，从而得出药物治疗更有效的错误结论。而事实上，通过潜在结果计算出的平均因果效应，手术治疗要比药物治疗寿命长 2 年。

根据分配机制是否已知，可以将分配机制分成两类：

1. 随机实验：分配机制是由实验者控制的，是已知的；
2. 观测研究：分配机制是未知的，观测研究的目的就是想办法识别出未知的分配机制，从而估计因果效应；

协变量

为了搞清楚分配机制，往往需要一些协变量（Covariates），也称混淆变量（Confusion variable），协变量的基本特征是这些变量不受干预变量的影响，但是却往往决定个体的干预状态，协变量包括两种：

1. 个体属性：不随干预状态变化而变化的变量，比如性别、民族等变量；
2. 干预实施之前取值的变量：比如研究培训的作用时，培训前的收入水平及经济社会特征等；

条件独立性

非混杂性（Unconfoundedness），也称为条件独立性（Conditional independence），是指控制协变量 $X_i$ 后，个体干预状态的分配独立于潜在结果，非混杂性可以表示为：

$$(Y_{0i},Y_{1i})\perp D_i|X_i \tag {3}$$

根据分配机制是否满足条件独立性条件，可以将分配机制分成三类：

1. 经典随机化实验：分配机制满足条件独立性，且函数形式已知；
2. 规则分配机制（Regular assignment mechanism）：分配机制满足条件独立性，但函数形式未知；
3. 不规则机制（Irregular assignment mechanism）：分配机制不满足条件独立性；

Lord 悖论

潜在结果的概念，对理清所要研究的因果问题、定义因果效应非常有帮助。有些因果问题的探讨，必须从潜在结果概念出发才能搞清楚因果效应是否有清晰的定义，从观测结果出发进行建模往往不能清晰地表述所研究的因果效应问题。

这一节介绍一个在统计学中很有名，但是在中文统计教科书中几乎从未介绍过的悖论 —— Lord 悖论（Lord’s Paradox）。这个悖论是由美国教育考试服务中心（EducationalTestingService, ETS）统计学家 FredericLord 于 1967 年提出来的，最终由同在 ETS 工作的另外两位统计学家 Paul Holland 和 Donald Rubin 于 1982 年圆满地找出了这个悖论的根源。

悖论描述

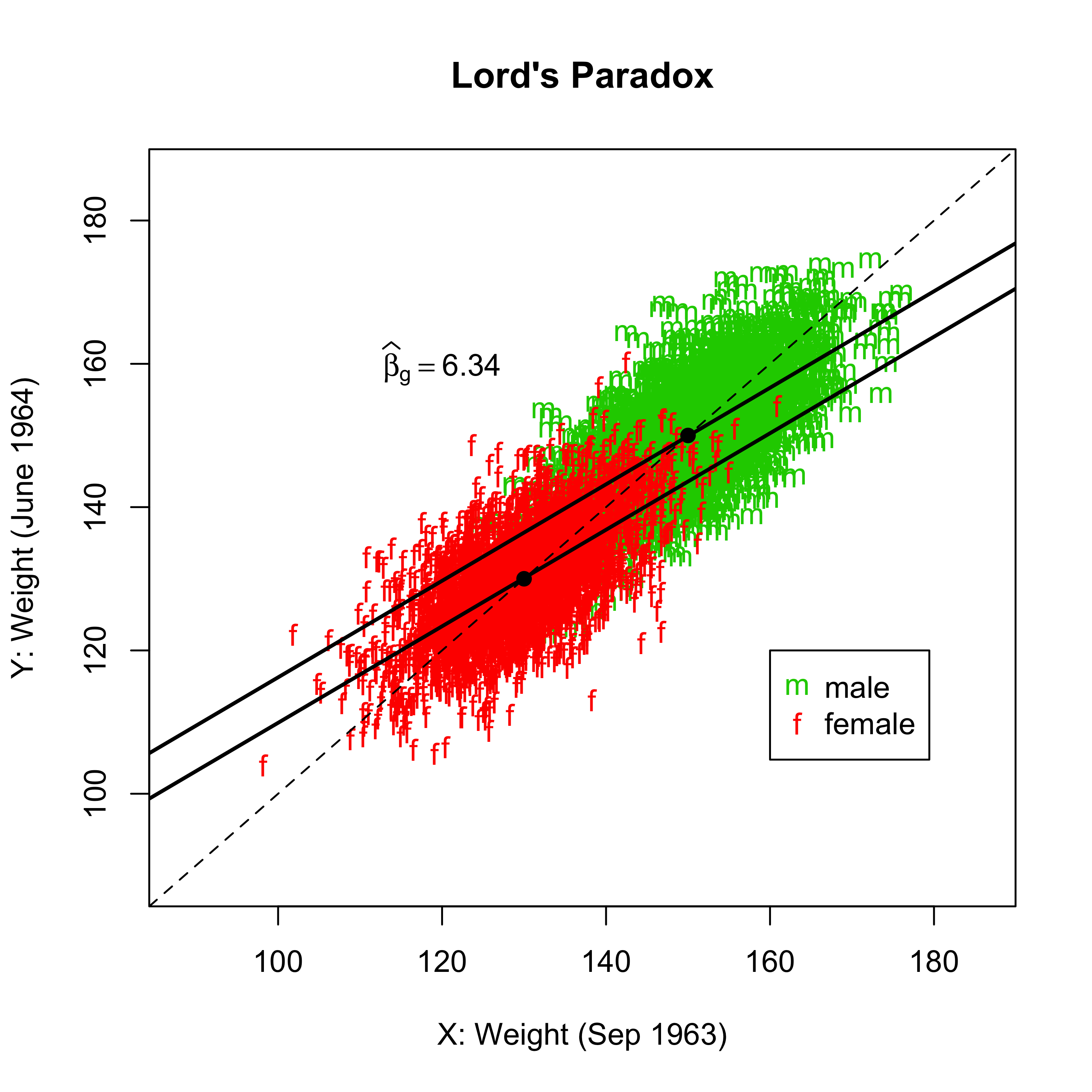
Lord（1967）构造了一个假想的案例，一所大学想考察其食堂膳食对于学生体重是否有差异性的影响，尤其关心食堂对于男女学生体重影响是否相同，为此，收集了学生 9 月份入学时的体重，然后次年 6 月份又获得了学生在校一学年后的体重。两个统计学家分别利用这个数据考察了学校食堂对学生体重的影响，但得到了完全不同的结论：

1. 第一个统计学家用了比较初等的方法，计算了男生和女生入学时的平均体重，分别是 150 磅和 130 磅。然后又计算了入学一学年后男、女生的平均体重，发现仍然是 150 磅和 130 磅。因而，第一位统计学家认为学生食堂膳食对学生体重没有影响。
2. 第二个统计学家采用了更加高等的方法 —— 回归分析，他认为为了考察食堂对学生体重的影响，必须比较两个初始体重相同的人，因而，他构造了一个回归模型，控制了个体入学时的体重，并考察了性别的差异。回归结果表明，同样体重的男生、女生相比，男生的体重增加更大，比女生平均高 7.3 磅。

两个统计学家利用同一数据，采用不同的方法，得到几乎相反的结果，一个说无因果影响，一个说对男生的影响更大，这种矛盾的结果被称为 Lord 悖论。那么，这两个统计学家的分析，哪一个正确呢？

悖论解释

我们首先用 Rubin 因果模型的框架套用到该问题上：

表中的问号（?）是解决 Lord 悖论的关键，尽管积极干预是非常清晰的——学校食堂膳食，它对学生体重的影响是想要研究的问题，但没有清晰的控制干预，不在学校食堂吃饭时是在家吃饭还是在外面下馆子，我们并不清楚，这意味着潜在结果 $Y_0$ 的定义是模糊的，我们权且将 $Y_0$ 看做是假如期间学生没有在学校食堂吃饭时的体重。然而，没有学生在控制组，所有学生都在学校食堂吃饭，为了回答食堂对学生体重的影响，必然要引入一些有关 $Y_0$ 的不可检验的假设，这也正是两位统计学家产生分歧的地方。

食堂膳食对学生体重的个体影响可以写作 $Y_1 - Y_0$，对男女学生的平均影响可以写作:

$$\Delta_i = E[Y_1-Y_0|G=i],\ i=1,2 \tag {4}$$

平均因果影响的性别差异为：

$$\begin{align*} \Delta &= \Delta_1 - \Delta_2\\ &=E[Y_1-Y_0|G=1]-E[Y_1-Y_0|G=2]\\ &=(E[Y_1|G=1]-E[Y_1|G=2])-(E[Y_0|G=1]-E[Y_0|G=2]) \end{align*} \tag {5}$$

第一位统计学家根据男女学生入学前和放假后平均体重的对比，得到学校膳食没有影响的结论。他所依据的假设是“假如学生不在学校食堂吃饭，他们的体重变化相同”，即 $Y_0 = X + C$，其中 $C$ 对男女学生都是相同的常量，基于该假设可以计算平均因果影响的性别差异：

$$\begin{align*} \Delta &= \Delta_1 - \Delta_2\\ &=E[Y_1-Y_0|G=1]-E[Y_1-Y_0|G=2]\\ &=E[Y_1-X-C|G=1]-E[Y_1-X-C|G=2]\\ &=E[Y_1-X|G=1]-E[Y_1-X|G=2]\\ &=0-0\\ &=0 \end{align*} \tag {6}$$

第二位统计学家认为应该控制开学时的体重，比较相同体重的人放假时体重的变化，对于初始体重为 X 的个体，体重的增加为 $\delta_i(X) = E[Y_i-X|X,G=i],\ i=1,2$，增量的性别差异为 $\delta(X) = \delta_1(X)-\delta_2(X)$，为简单起见，Lord 假设条件期望函数均为线性且男女生斜率相同，即 $E[Y_i|X,G=i]=a_i+bX,\ i=1,2$，则 $\delta(X)=a_1-a_2$。$\delta(X)$ 与因果效应参数 $\Delta$ 没有直接关系，但是在一定的假设下二者等价，比如假设“如果学生不在学校食堂吃饭，他们的体重是初始体重的线性函数”，即 $Y_0 = a + bX$，并且对所有性别的学生都一样，在此假设下，有：

$$\begin{align*} \Delta &= \Delta_1 - \Delta_2\\ &=E[Y_1-Y_0|G=1]-E[Y_1-Y_0|G=2]\\ &=E[Y_1-a-bX|G=1]-E[Y_1-a-bX|G=2]\\ &=E[Y_1-bX|G=1]-E[Y_1-bX|G=2]\\ &=E[E[Y_1|X,G=1]-bX|G=1]-E[E[Y_1|X,G=2]-bX|G=2]\\ &=E[a_1+bX-bX|G=1]-E[a_2+bX-bX|G=2]\\ &=a_1-a_2\\ \end{align*}\tag {7}$$

关于 Lord’s Paradox，我们有如下结论：

1. Lord 悖论的根源在于整个研究没有控制组，我们甚至不知道什么是控制组，这导致 $Y_0$ 定义模糊；
2. 统计学家一和二，都可能是对的，他们结论的正确性，依赖于不同的假定，而这些假定本身是不可能被检验的；
3. 统计学家一和二，都是错的，他们有结论，但是却从未清楚地陈述结论回答的是什么问题；
4. 潜在结果的概念，对理清所要研究的因果问题、定义因果效应非常有帮助；

因果效应参数

ATE & ATT & ATC 定义

实证研究中，我们关心的往往不是某一特定个体的因果效应，而是干预的平均因果效应。假设有 N 个个体，用 i=1,……,N 表示，$D_i \in {0,1}$ 表示干预变量，个体因果效应为：

$$\tau_i=Y_{1i}-Y_{0i},\ i=1,\cdots ,N \tag {8}$$

个体因果效应往往无法估计，因而，我们关注总体平均因果效应（Average Treatment Effect, ATE），它表示从总体中随机抽取一个个体进行干预的平均因果效应：

$$\tau_{ATE}=E[Y_{1i}-Y_{0i}] \tag {9}$$

在政策评价中，我们更关心那些受到政策影响的个体的平均因果效应，称为干预组平均因果效应（Average Treatment Effect for the Treated,ATT）：

$$\tau_{ATT}=E[Y_{1i}-Y_{0i}\mid D_i=1] \tag {10}$$

有些时候，我们关注那些没有受到政策影响的个体如果接受政策干预的话，其平均因果效应是多少，称为控制组平均因果效应（Average Treatment Effect for the Control, ATC）：

$$\tau_{ATC}=E[Y_{1i}-Y_{0i}\mid D_i=0] \tag {11}$$

不同的因果效应参数回答不同的问题，比如考察大学教育对个体收入的影响，将大学教育看作一项积极干预，高中教育看作一项控制干预：

1. ATE：如果想知道大学教育对所有国民的平均影响，估计的参数是总体的平均因果效应（ATE），它反映的是如果全部国民均接受大学教育相对于均接受高中教育全部国民的平均收入增长。
2. ATT：如果关心的政策问题是大学教育给接受者带来了多大程度的收入增加，需要估计的参数是干预组平均因果效应（ATT）。
3. ATC：如果想知道那些仅完成高中教育的个人，如果他们能够完成大学教育的话，他们的收入将增长多少，则需要估计的参数是控制组平均因果效应（ATC）。

ATE & ATT & ATC 计算

下面通过一个简单的例子来示范三个因果效应参数的计算，假设有四个个体，并且我们可以同时看到两种干预状态下的潜在结果（现实中只能看到一种状态下的结果）:

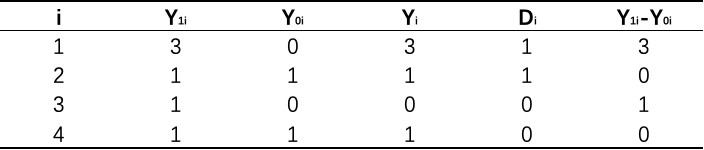
理论上，我们可以根据表中的潜在结果数据分别计算 ATE、ATT、ATC：

$$\begin{align*} \tau_{ATE}&=E[Y_{1i}-Y_{0i}]=3\cdot 1/4 + 0 \cdot 1/4 + 1 \cdot 1/4 + 0 \cdot 1/4=1.0\\ \tau_{ATT}&=E[Y_{1i}-Y_{0i}\mid D_i=1]=3\cdot 1/2 + 0 \cdot 1/2=1.5\\ \tau_{ATC}&=E[Y_{1i}-Y_{0i}\mid D_i=0]=1\cdot 1/2 + 0 \cdot 1/2=0.5 \end{align*}$$

实际上，我们仅能观测到每个个体在其中一种状态下的潜在结果。对于前两个个体，他们在干预组，我们可以观测到他们在积极干预状态下的潜在结果 $Y{1i}=Y_i$，但观测不到他们在控制状态下的潜在结果 $Y{0i}$；相反对于后两个个体，他们在控制组，我们可以观测到他们在被动控制状态下的潜在结果 $Y{0i}=Y_i$，但却观测不到他们在干预状态下的潜在结果 $Y{1i}$。从而，前面计算的三个因果效应参数也就没有办法计算出来了，现在我们再来看各个因果效应参数的定义：

$$\begin{align*} \tau_{ATE}&=E[Y_{1i}-Y_{0i}]\\ &=E[E[Y_{1i}-Y_{0i}|D_i]]\\ &=E[Y_{1i}-Y_{0i}|D_i=1]\cdot P(D_i=1)+E[Y_{1i}-Y_{0i}|D_i=0]\cdot P(D_i=0) \\ &=\tau_{ATT}\cdot P_t+\tau_{ATC}\cdot P_c\\ \tau_{ATT}&=E[Y_{1i}-Y_{0i}|D_i=1]=E[Y_i|D_i=1]-E[Y_{0i}|D_i=1]\\ \tau_{ATC}&=E[Y_{1i}-Y_{0i}|D_i=0]=E[Y_{1i}|D_i=0]-E[Y_i|D_i=0] \end{align*}\tag {12}$$

其中，反事实结果 $E[Y{0i}|D_i=1]$ 和 $E[Y{1i}|D_i=0]$ 是观测不到的，必须通过一定的方法将其估计出来，才能得到以上干预效应。

回归分析与因果效应

学过回归分析的学生可能禁不住想用 $Y_i$ 对 $D_i$ 回归，这也是计量经济学的基本建模方式，但是这种回归并不能识别出任何因果效应参数。比如我们建立一个简单的双变量回归模型：

$$Y_i=\alpha + \tau D_i + \varepsilon_i \tag {13}$$

根据初等计量经济学的知识，用一个容量为 N 的随机样本去估计上述简单回归模型，$D_i$ 的回归系数为：

$$\hat{\tau}^{ols}=\frac{\sum_{i=1}^{N}(Y_i-\bar{Y})(D_i-\bar{D})}{\sum_{i=1}^{N}(D_i-\bar{D})^2} \tag {14}$$

当干预变量是 $0-1$ 二值变量时，可以证明 $Y_i$ 对 $D_i$ 的回归系数 $\hat{\tau}^{ols}$ 等于干预组和控制组样本均值之差，在大样本的情况下：

$$\hat{\tau}^{ols}=\bar{Y_t}-\bar{Y_c}\overset{p}{\rightarrow}E[Y_i|D_i=1]-E[Y_i|D_i=0]=\tau^{ols} \tag {15}$$

$\tau^{ols}$ 是总体回归系数，一般不能反映因果效应参数，除非施加一定的假设。

首先，考察总体回归系数和干预组平均因果效应（ATT）之间的关系：

$$\begin{align*} \tau^{ols}&=E[Y_i|D_i=1]-E[Y_i|D_i=0]\\ &=E[Y_{1i}|D_i=1]-E[Y_{0i}|D_i=0]\\ &=E[Y_{1i}-Y_{0i}|D_i=1]+(E[Y_{0i}|D_i=1]-E[Y_{0i}|D_i=0])\\ &=\tau_{ATT}+\Delta \tau_0 \end{align*} \tag {16}$$

回归系数和因果效应参数 ATT 之间相差 $E[Y{0i}｜D_i=1]-E[Y{0i}｜Di=0]$，它表示干预组和控制组个体在控制状态下的潜在结果差异，也称为基线潜在结果差异（difference in baseline potential outcomes），这一偏差通常称为选择偏差（selection bias）。$E[Y{0i}｜Di=1]$ 表示干预组个体在控制状态下的潜在结果，是观测不到的，但是在选择偏差为 0 的假设下，可以用控制组的观测结果 $E[Y{0i}｜Di=0]$ 来代替干预组的反事实结果 $E[Y{0i}|D_i=1]$。比如教育收益率的例子，如果潜在收入高的人倾向于选择上大学，那么，上大学的人即使仅完成了高中教育，他们的收入也会比高中组高，那么大学组合高中组观测到的收入均值差就不能解释为大学教育对个人收入的因果影响，选择偏差为正，回归系数将高估教育对收入的影响。

类似地，总体回归系数也不是控制组平均因果效应（ATC），只有假设干预组和控制组的干预潜在结果相同，即 $E[Y{1i}|D_i=1]=E[Y{1i}|D_i=0]$，回归系数才等于 ATC：

$$\begin{align*} \tau^{ols}&=E[Y_i|D_i=1]-E[Y_i|D_i=0]\\ &=E[Y_{1i}|D_i=1]-E[Y_{0i}|D_i=0]\\ &=E[Y_{1i}-Y_{0i}|D_i=0]+(E[Y_{1i}|D_i=1]-E[Y_{1i}|D_i=0])\\ &=\tau_{ATC}+\Delta \tau_1 \end{align*} \tag {17}$$

最后，总体回归系数通常也不是平均因果效应，只有同时施加假设 $\Delta \tau0=0$ 和$\Delta \tau_1=0$ 时，总体回归系数才可解释为总体平均因果效应。将式 $(16)$ 和 $(17)$ 带入到 $\tau{ATE}=\tau{ATT}\cdot P_t+\tau{ATC}\cdot P_c$，易得：

$$\tau^{ols}=\tau_{ATE}+\Delta \tau_0+P_c\cdot (\tau_{ATT}-\tau_{ATC}) \tag {18}$$

我们可以得到分配机制、潜在结果、干预效应和回归系数之间的一般关系，如下图所示：

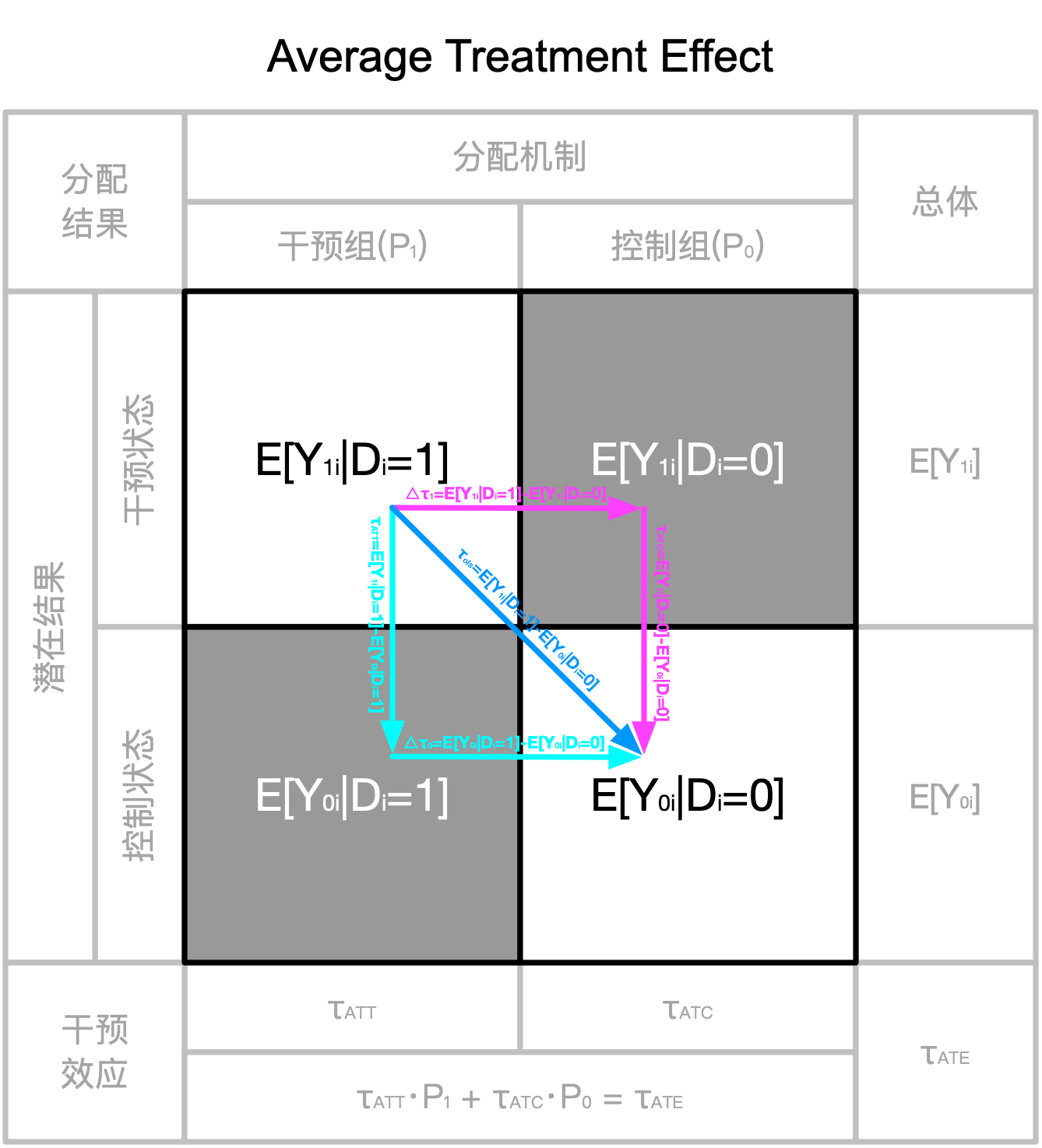
需要注意的是，潜在结果框架仅关注因果效应，不能说明变量之间的影响机制，因果效应是一个“黑箱”，只能给出因果效应的大小，不能给出产生这一因果效应的内在机制。

参考

• 赵西亮. 基本有用的计量经济学 (高等院校经济学管理学系列教材)
• 因果推断简介之七：Lord’s Paradox